Question

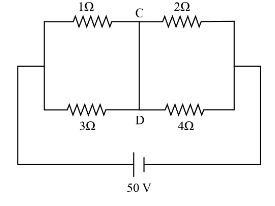
In the given circuit diagram, find the current passing through the wire CD (in ampere): -

A. 1
B. 2
C. 3
D. 4

Answer 1

Hint:The above problem can be resolved using the concepts and the applications of the circuit analysis. In carrying out the complex circuit analysis, the fundamental formulas of the Ohm's law are also applied. Ohm's law involved in this problem will be carried out for every segment of the circuit. Moreover, the value for the voltage supply is calculated using the loop rule, and on further substitution, the amount of the current is obtained.

Complete step by step answer:
Given:
The value of first resistance is, \[{R_1} = 1\;\Omega \].
The value of second resistance is, \[{R_2} = 2\;\Omega \].
The value of third resistance is, \[{R_3} = 3\;\Omega \].
The value of fourth resistance is, \[{R_4} = 4\;\Omega \].
The voltage supply through the battery is, \[{V_1} = 50\;{\rm{V}}\].
 Let V be the voltage through the CD. Then apply the loop rule in the given circuit as,
\[{I_1} + {I_2} + {I_3} + {I_4} = 0\] …….. (1)
Here, the variables are represented as,
\[{I_1}\] is the current through the resistance of 1 ohms and its value is, \[\dfrac{{50\;{\rm{V}} - V}}{{1\;\Omega }}\]…….(2)
\[{I_2}\] is the current through the resistance of 2 ohms and its value is, \[\dfrac{V}{{2\;\Omega }}\]…….. (3)
\[{I_3}\] is the current through the resistance of 3 ohms and its value is, \[\dfrac{{50\;{\rm{V}} - V}}{{3\;\Omega }}\]…..…(4)
\[{I_4}\] is the current through the resistance of 4 ohms and its value is, \[\dfrac{V}{{4\;\Omega }}\]…….…(4)
Solve by substituting the values in equation 1 as,
\[\begin{array}{l}
{I_1} + {I_2} + {I_3} + {I_4} = 0\\
\dfrac{{50\;{\rm{V}} - V}}{{1\;\Omega }} + \dfrac{V}{{2\;\Omega }} + \dfrac{{50\;{\rm{V}} - V}}{{3\;\Omega }} + \dfrac{V}{{4\;\Omega }} = 0\\
V = 32\;{\rm{V}}
\end{array}\]
Now, the current through CD is,
\[\begin{array}{l}
{I_{CD}} = {I_1} - {I_2}\\
{I_{CD}} = \dfrac{{50\;{\rm{V}} - 32\;{\rm{V}}}}{{1\;\Omega }} - \dfrac{{32\;{\rm{V}}}}{{2\;\Omega }}\\
{I_{CD}} = 2\;{\rm{A}}
\end{array}\]
Therefore, the magnitude of current through CD is 2 A and option (B) is correct.

Note: Try to understand the concept of the circuit analysis and also go through the various methods, by which the circuit analysis is needed to carry out. Besides, the fundamentals of Ohm's law are also needed to remember.