
In the following shaded region, the linear constraints (except \[x \geqslant 0\]and\[y \geqslant 0\]) are:
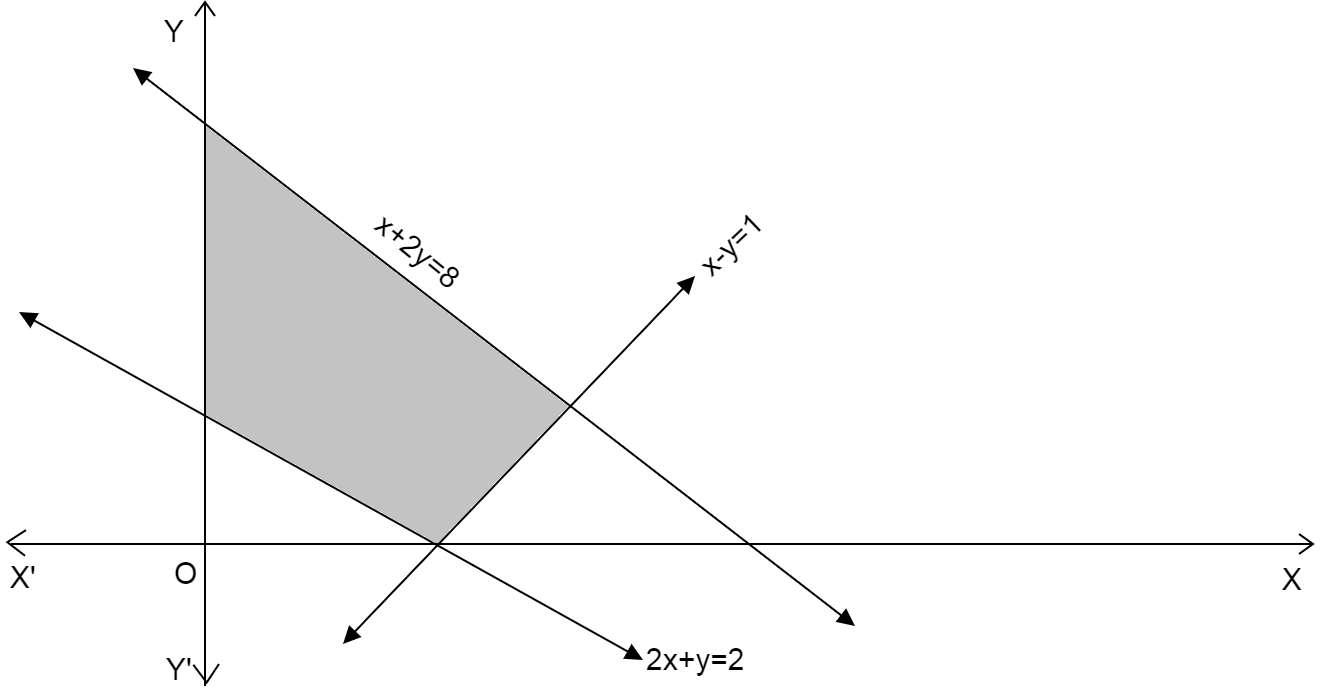
A.\[2x + y \leqslant 2,x - y \leqslant 1,x + 2y \leqslant 8\]
B.\[2x + y \geqslant 2,x - y \leqslant 1,x + 2y \leqslant 8\]
C.\[2x + y \leqslant 2,x - y \geqslant 1,x + 2y \leqslant 8\]
D.\[2x + y \leqslant 2,x - y \leqslant 1,x + 2y \geqslant 8\]

Answer
570.9k+ views
Hint: We use the concept of shading a region between the equations by comparing the signs ‘less than equal to (\[ \leqslant \])’ and ‘greater than equal to (\[ \geqslant \])’ between the equation and the constant value on the other side of the equation. Check the sign of inequality for each equation and choose the option that holds true for all the three equations.
* If the equation of the straight line is less than or equal to a constant, then shade the area below the line.
* If the equation of the straight line is greater than or equal to a constant then shade the area above the line.
Complete step by step answer:
We are given the figure where there are three straight lines \[2x + y = 2;x - y = 1;x + y = 8\]
The three straight lines intersect each other at some point and intersect the x-axis and y-axis.
The shaded region is in the first quadrant where both x coordinate and y coordinate are positive.
We have constraints \[x \geqslant 0\]and\[y \geqslant 0\]
We look at each line separately and check the inequality by considering a point.
First:
We consider the line \[x + 2y = 8\]
Since, the shaded region in the graph is below the line \[x + 2y = 8\]
We take the inequality \[x + 2y \leqslant 8\]
Check the inequality by considering a point.
Let \[(0,0)\]be the point. Since this point lies below the line it must satisfy the inequality.
\[ \Rightarrow (0) + 2(0) \leqslant 8\]
\[ \Rightarrow 0 \leqslant 8\]
Therefore the inequality for the line \[x + 2y = 8\] that represents the shaded region is \[x + 2y \leqslant 8\].
Second:
We consider the line \[x - y = 1\]
Since the shaded region in the graph is above the line \[x - y = 1\]
We take the inequality \[x - y \geqslant 1\]
Check the inequality by considering a point.
Let \[(0,0)\]be the point. Since this point lies above the line it must satisfy the inequality.
\[ \Rightarrow (0) - (0) \geqslant 1\]
\[ \Rightarrow 0 \geqslant 1\]
This is incorrect as the point above the line does not satisfy the inequality.
So we take the inequality \[x - y \leqslant 1\]
Therefore the inequality for the line \[x - y = 1\] that represents the shaded region is \[x - y \leqslant 1\].
Third:
We consider the line \[2x + y = 2\]
Since the shaded region in the graph is above the line \[2x + y = 2\]
We take the inequality \[2x + y \geqslant 2\]
Check the inequality by considering a point.
Let \[(1,1)\] be the point. Since this point lies above the line it must satisfy the inequality.
\[ \Rightarrow 2(1) + (1) \geqslant 2\]
\[ \Rightarrow 3 \geqslant 2\]
Therefore the inequality for the line \[2x + y = 2\] that represents the shaded region is \[2x + y \geqslant 2\].
From the three cases we get the set of constraints as: \[x + 2y \leqslant 8\]; \[x - y \leqslant 1\] and \[2x + y \geqslant 2\].
\[\therefore \] Option (B) is the correct option.
Note:
Students might get confused with the shaded region as it depicts the inequality \[x - y \geqslant 1\] for the line \[x - y = 1\]. Keep in mind, we always check if the inequality holds true or not by considering a point above or below the line which should give the required result.
Also, many students try to find the points of intersections of three lines and then check the shaded region, this process is long and we have no use of points of intersection of lines in this solution.
* If the equation of the straight line is less than or equal to a constant, then shade the area below the line.
* If the equation of the straight line is greater than or equal to a constant then shade the area above the line.
Complete step by step answer:
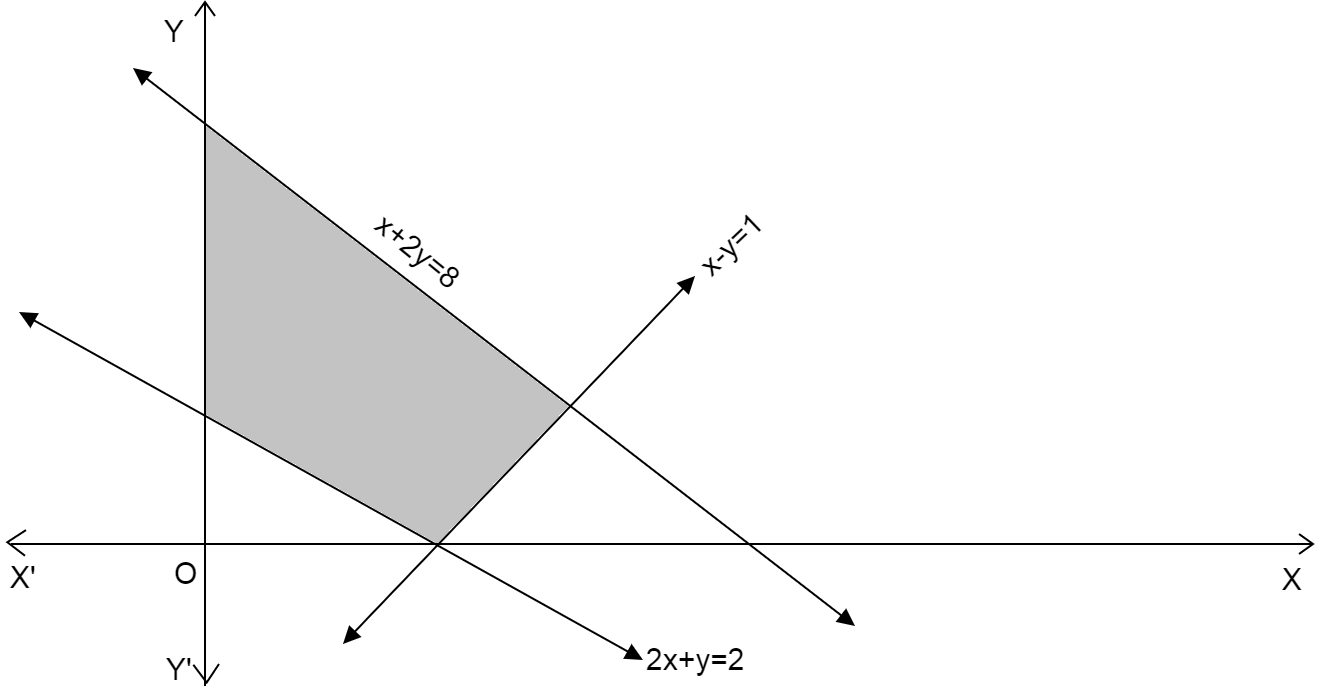
We are given the figure where there are three straight lines \[2x + y = 2;x - y = 1;x + y = 8\]
The three straight lines intersect each other at some point and intersect the x-axis and y-axis.
The shaded region is in the first quadrant where both x coordinate and y coordinate are positive.

We have constraints \[x \geqslant 0\]and\[y \geqslant 0\]
We look at each line separately and check the inequality by considering a point.
First:
We consider the line \[x + 2y = 8\]
Since, the shaded region in the graph is below the line \[x + 2y = 8\]
We take the inequality \[x + 2y \leqslant 8\]
Check the inequality by considering a point.
Let \[(0,0)\]be the point. Since this point lies below the line it must satisfy the inequality.
\[ \Rightarrow (0) + 2(0) \leqslant 8\]
\[ \Rightarrow 0 \leqslant 8\]
Therefore the inequality for the line \[x + 2y = 8\] that represents the shaded region is \[x + 2y \leqslant 8\].
Second:
We consider the line \[x - y = 1\]
Since the shaded region in the graph is above the line \[x - y = 1\]
We take the inequality \[x - y \geqslant 1\]
Check the inequality by considering a point.
Let \[(0,0)\]be the point. Since this point lies above the line it must satisfy the inequality.
\[ \Rightarrow (0) - (0) \geqslant 1\]
\[ \Rightarrow 0 \geqslant 1\]
This is incorrect as the point above the line does not satisfy the inequality.
So we take the inequality \[x - y \leqslant 1\]
Therefore the inequality for the line \[x - y = 1\] that represents the shaded region is \[x - y \leqslant 1\].
Third:
We consider the line \[2x + y = 2\]
Since the shaded region in the graph is above the line \[2x + y = 2\]
We take the inequality \[2x + y \geqslant 2\]
Check the inequality by considering a point.
Let \[(1,1)\] be the point. Since this point lies above the line it must satisfy the inequality.
\[ \Rightarrow 2(1) + (1) \geqslant 2\]
\[ \Rightarrow 3 \geqslant 2\]
Therefore the inequality for the line \[2x + y = 2\] that represents the shaded region is \[2x + y \geqslant 2\].
From the three cases we get the set of constraints as: \[x + 2y \leqslant 8\]; \[x - y \leqslant 1\] and \[2x + y \geqslant 2\].
\[\therefore \] Option (B) is the correct option.
Note:
Students might get confused with the shaded region as it depicts the inequality \[x - y \geqslant 1\] for the line \[x - y = 1\]. Keep in mind, we always check if the inequality holds true or not by considering a point above or below the line which should give the required result.
Also, many students try to find the points of intersections of three lines and then check the shaded region, this process is long and we have no use of points of intersection of lines in this solution.
Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
Differentiate between an exothermic and an endothermic class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

State the laws of reflection of light




