Answer
377.4k+ views
Hint:All that is required is the balancing of the forces. The net external force is equal to the sum of the forces acting on the object. Also keep in mind the tension force which comes along whenever strings/ropes are into play.
Complete step by step answer:
According to Newton’s second law of motion, $F=ma$ where $F$ is the net external force, m is the mass of the body and $a$ is the acceleration with which the body moves. According to Newton’s third law of motion,to every action there is an equal and opposite reaction force.We know that all physical objects that are in contact can exert forces on each other.Tension is the force exerted by a rope,string,chain etc.Tension is a pulling force transmitted along the axis.
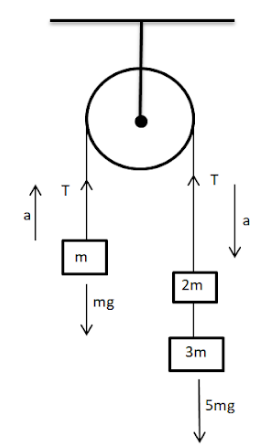
For an object with mass m, the net external force acting on it is the sum of all the forces acting on the object. And according to the second law, net external force is equal to ma.
Let $T$ be the tension in the string going over the pulley. Therefore $ma=T+(-mg)$.......[$mg$ is in the opposite direction to that of the external force,hence a negative sign.]
$T-mg=ma$
$\Rightarrow T=ma+mg$--equation $1$
Let us consider the right hand masses as a single unit of mass $5$m ($3$m+$2$m). For an object with mass $5m$, the net external force acting on it is the sum of all the forces acting on the object. Net external force is equal to 5ma. (According to second law)
Therefore $5$ma=$5$mg+(-T )......[ T is in the opposite direction to that of the external force.]
$5mg-T=5ma$
$\Rightarrow 5mg-5ma=T$--equation 2
Substituting value of $T$ from equation 1 in equation 2, we get
$5mg-5ma=ma+mg$
$\Rightarrow 5mg-mg=ma+5ma$
$\Rightarrow 4mg=6ma$
$\Rightarrow a=\dfrac{4g}{6}$
$\therefore a=\dfrac{2g}{3}$
Hence the acceleration of the block of mass $m$ is $\dfrac{2g}{3}$.
Note:Two or more physical objects that are in contact, exert forces on each other.Based on the objects in contact we give these contact forces different names. If one of these objects in contact happens to be a string, rope, cable or spring, we call the force as tension.
Complete step by step answer:
According to Newton’s second law of motion, $F=ma$ where $F$ is the net external force, m is the mass of the body and $a$ is the acceleration with which the body moves. According to Newton’s third law of motion,to every action there is an equal and opposite reaction force.We know that all physical objects that are in contact can exert forces on each other.Tension is the force exerted by a rope,string,chain etc.Tension is a pulling force transmitted along the axis.

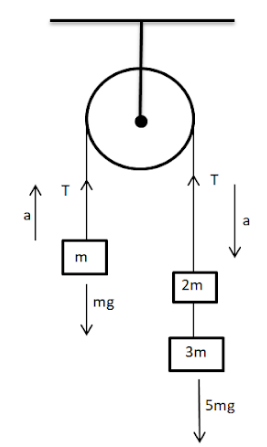
For an object with mass m, the net external force acting on it is the sum of all the forces acting on the object. And according to the second law, net external force is equal to ma.
Let $T$ be the tension in the string going over the pulley. Therefore $ma=T+(-mg)$.......[$mg$ is in the opposite direction to that of the external force,hence a negative sign.]
$T-mg=ma$
$\Rightarrow T=ma+mg$--equation $1$
Let us consider the right hand masses as a single unit of mass $5$m ($3$m+$2$m). For an object with mass $5m$, the net external force acting on it is the sum of all the forces acting on the object. Net external force is equal to 5ma. (According to second law)
Therefore $5$ma=$5$mg+(-T )......[ T is in the opposite direction to that of the external force.]
$5mg-T=5ma$
$\Rightarrow 5mg-5ma=T$--equation 2
Substituting value of $T$ from equation 1 in equation 2, we get
$5mg-5ma=ma+mg$
$\Rightarrow 5mg-mg=ma+5ma$
$\Rightarrow 4mg=6ma$
$\Rightarrow a=\dfrac{4g}{6}$
$\therefore a=\dfrac{2g}{3}$
Hence the acceleration of the block of mass $m$ is $\dfrac{2g}{3}$.
Note:Two or more physical objects that are in contact, exert forces on each other.Based on the objects in contact we give these contact forces different names. If one of these objects in contact happens to be a string, rope, cable or spring, we call the force as tension.
Recently Updated Pages
How many sigma and pi bonds are present in HCequiv class 11 chemistry CBSE

Mark and label the given geoinformation on the outline class 11 social science CBSE

When people say No pun intended what does that mea class 8 english CBSE

Name the states which share their boundary with Indias class 9 social science CBSE

Give an account of the Northern Plains of India class 9 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

In Indian rupees 1 trillion is equal to how many c class 8 maths CBSE

Which are the Top 10 Largest Countries of the World?

How do you graph the function fx 4x class 9 maths CBSE

Give 10 examples for herbs , shrubs , climbers , creepers

Difference Between Plant Cell and Animal Cell

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE