Question

In the circuit shown above, the key is pressed at time t=0. Which of the following statement(s) is(are) true?

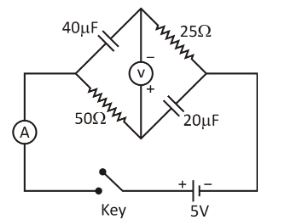
A. The voltmeter displays -5V as soon as the key is pressed and displays +5V after a long time
B. The voltmeter will display 0V at time t=ln2 seconds
C. The current in the ammeter becomes 1/e of the initial value after 1 second
D. The current in the ammeter becomes zero after a long time.

Answer 1

Hint:You need to understand the behaviour of the capacitor with time at starting time or t=0 capacitor acts as a plane wire and at end time or $t = \infty $ capacitor acts as a open wire so at t=0 both the resistor will be in parallel as voltage across them will be same and at $t = \infty $ both the resistance will be in series as there will be no current in capacitors.

Complete step by step answer:
Let at an instant ${q_1}$ be charged on upper and ${q_2}$ be charged on the lower capacitor. Then,
${q_1} = 40 \times {10^{ - 6}}5(1 - {e^{ - t}})\\
\Rightarrow {q_1} = 200 \times {10^{ - 6}}(1 - {e^{ - t}})$ and
$\Rightarrow {q_2} = 20 \times {10^{ - 6}} \times 5(1 - {e^{ - t}})\\
\Rightarrow {q_2} = 100 \times {10^{ - 6}}(1 - {e^{ - t}})$
Using ohm's law
$V = IR$
We have,
$\dfrac{{{q_1}}}{C} = R\dfrac{{d{q_2}}}{{dt}}$
Putting the value of into the formula we have
\[\dfrac{{200 \times {{10}^{ - 6}}(1 - {e^{ - t}})}}{{40 \times {{10}^{ - 6}}}} = 50 \times {10^3}\dfrac{d}{{dt}}(100 \times {10^{ - 6}}(1 - {e^{ - t}}))\]
$ \Rightarrow \dfrac{{200 \times {{10}^{ - 6}}(1 - {e^{ - t}})}}{{40 \times {{10}^{ - 6}}}} = 50 \times {10^3} \times 100 \times {10^{ - 6}}{e^{ - t}}$
$ \Rightarrow 10{e^{ - t}} = 5\\
\Rightarrow {e^{ - t}} = 0.5\\
\Rightarrow t = \ln 2$
Hence option-B is correct

Let total current in the circuit be I then,
$I = {I_1} + {I_2}$
Putting the values we have,
$I = \dfrac{d}{{dt}}\left( {200 \times {{10}^{ - 6}}(1 - {e^{ - t}})} \right) + \dfrac{d}{{dt}}(100 \times {10^{ - 6}}(1 - {e^{ - t}}))$
$ \Rightarrow I = 200 \times {10^{ - 6}}{e^{ - t}} + 100 \times {10^{ - 6}}{e^{ - t}}$
$\Rightarrow I = 0.0003{e^{ - t}}$
At $t = 0$, $I = 0.0003$
And at $t = 1,$$I = \dfrac{{0.0003}}{e}$
So option C is correct.

At t=0 current there will potential across voltmeter will be same as source voltage only polarity will be reversed so it will read -5V and at $t = \infty $ there will be no current in the circuit as ideal voltmeter has infinite resistance so, it will read +5V

For option A and option D you can simply use an analogy to find whether it is correct or not but for the other two options you will have to write an equation and solve for it. There is no other shortcut way you can do it using basics too but it's better to use formulas for less complexity.

Hence Option-ABCD are correct.

Note: Sometimes students try to solve this question using fundamentals but it will be very hard and complex if you use simple kirchhoff's laws because so you should always look for tricks if possible in such types of questions, if no trick is applied then you can use fundamentals.