Question

In the arrangement shown in the figure, the current through $5\Omega$ resistor is?

\[\begin{align}
  & A.2A \\
 & B.0 \\
 & C.\dfrac{12}{7}A \\
 & D.1A \\
\end{align}\]

Answer 1

Hint: The value of $I$, flowing through the $5\Omega$ resistance can be found using Kirchhoff’s laws. Assume the directions of current and solve the Kirchhoff equations. Negative sign in the current implies the current flows in the opposite direction.
Formula:
\[V=IR\]
 ( Ohm’s law).

Complete answer:
Kirchhoff’s Current Law or Kirchhoff’s First Law or Kirchhoff’s Junction Rule, states that in any circuit, the total of the currents in any junction is equal to the sum of currents outside the junction.
Kirchhoff’s Voltage Law or Kirchhoff’s Second Law or Kirchhoff’s Loop Rule. According to the loop rule, the sum of the voltages around any closed loop is equal to zero or null.
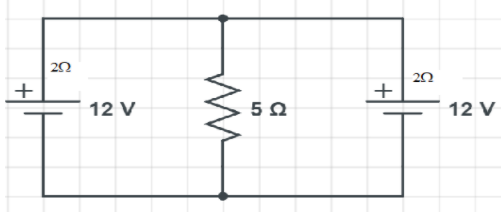
Let us consider the direction of the current as shown in the figure below.

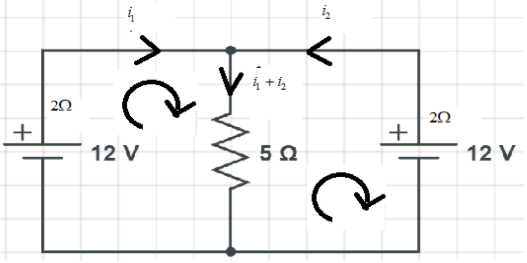
Defining the conventions:

From the voltage law in the first loop, we have,
$2i_{1}+5(i_{1}+i_{2})=12$
$\implies 7i_{1}+5i_{2}=12$
Similarly, in the loop 2, we have
$2i_{2}+5(i_{1}+i_{2})=12$
$\implies 7i_{2}+5i_{1}=12$
From the two equation, multiplying $7$ and $5$ to equation (1.1) and (1.2) respectively, we have
$\implies 49i_{1}+35i_{2}=84$ and $\implies 25i_{1}+35i_{2}=60$
On solving, we get,
$\implies 49i_{1}+60-25i_{1}=84$
$\implies 24i_{1}=24$
$\implies i_{1}=1A$
From (1.1) we get, $i_{2}=\dfrac{12-7}{5}=1A$
Hence the current flowing via $5\Omega$ is $i_{1}+i_{2}=2A$

Thus the correct answer is option $A.\;2\;A$

Additional information:
In 1845, a German physicist, Gustav Kirchhoff developed Kirchhoff's laws that deal with the conservation of current and energy within any electrical circuits. These two laws are commonly known as Kirchhoff’s Voltage and Current Laws. The advantages of the laws are:
It makes the calculation of unknown voltages or currents easy.
The analysis and simplification of complex closed-loop in the circuits are reduced and becomes manageable.

Note:
To begin with, let us assume the directions of current and solve the Kirchhoff equations. If there is a negative sign in the current, it implies that the current flows in the opposite direction. Also take care of the sign convention which is used in the calculation. Loops can be taken in the clockwise or anticlockwise direction. Use \[V=IR\] Ohm's law.