
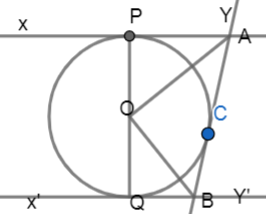
In figure, XY and X'Y' are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X'Y' at B. Prove that

Answer
604.8k+ views
Hint: In this question, we need to draw the diagram clearly in order to understand the relation between the angles. We need to use the similarity property and the properties of two parallel lines with a transversal.
Complete step-by-step Solution:
Let us look at some of the basic definitions.
CIRCLE: Circle is defined as the locus of a point which moves in a plane such that its distance from a fixed point in that plane is constant.
TANGENT: In geometry, a tangent line to a circle is a line that touches the circle at exactly one point, never entering the circle's interior
CONGRUENCE OF TRIANGLES:
Two triangles that are identical in all respects are said to be congruent and are denoted by the symbol \[\cong \]. In two congruent triangles,
The corresponding sides are equal.
The corresponding angles are equal.
Conditions for two triangles to be congruent:
Three sides of one triangle are respectively equal to three sides of the second triangle (SSS).
Two sides and the included angle of one triangle respectively equal to two sides and the included angle of another triangle (SAS).
Two angles and the included side of one triangle are respectively equal to two angles and the included side of another triangle (ASA).
Two right angled triangles are congruent, if the hypotenuse and one side of one triangle are respectively equal to the hypotenuse and one side of another right angled triangle (RHS).
Now, let us look at the diagram clearly,
As we already know that tangent to a circle is perpendicular to the radius of circle at the point of contact.
\[OP\bot XY\]
\[OC\bot AB\]
In triangle OPA and OCA
\[\angle OPA=\angle OCA={{90}^{\circ }}\]
As they are tangents to the circle at points P and C.
\[OP=OC\]
As they are radii of the same circle.
\[AP=AC\]
We already know that lengths of the tangent from an external point are equal.
Now, by observing the above conditions from SAS congruence we can say that,
\[\therefore \vartriangle OPA\cong \vartriangle OCA\]
\[\therefore \angle OAP=\angle OAC\]
\[\therefore \angle OAC=\dfrac{1}{2}\angle PAC\]
Similarly, we can also say that.
\[\begin{align}
& \angle OBC=\angle OBQ \\
& \angle OBC=\dfrac{1}{2}\angle QBC \\
\end{align}\]
As we know that XY and X'Y' are parallel. So, here AB acts as a transversal.
We already know that sum of the interior angles on the same side of a transversal is
\[{{180}^{\circ }}\]
\[\angle PAB+\angle QBA={{180}^{\circ }}\]
Similarly, by considering the other part we get,
\[\angle PAC+\angle QBC={{180}^{\circ }}\]
On diving with 2 on both sides the above equation becomes:
\[\dfrac{1}{2}\left( \angle PAC+\angle QBC \right)={{90}^{\circ }}\]
\[\angle OAC+\angle OBC={{90}^{\circ }}\]
\[\left[ \because \angle OAC=\angle OAB,\angle OBC=\angle OBA \right]\]
From triangle OAB we can write,
\[\begin{align}
& \angle AOB+\angle OAB+\angle OBA={{180}^{\circ }} \\
& \angle AOB={{180}^{\circ }}-\left( \angle OAB+\angle OBA \right) \\
& \angle AOB={{180}^{\circ }}-{{90}^{\circ }} \\
& \therefore \angle AOB={{90}^{\circ }} \\
\end{align}\]
Note:
In order to prove the congruence you need to look at all the sides and angles which are equal because neglecting one of them changes the rule of congruence.
As we know that the line joining the centre and the external point from where tangents are drawn to the circle bisects the angle formed at the external point to the circle.
\[\angle OAP=\angle OAC\]
It is important to note that AB acts as a transversal to the parallel lines XY and X'Y'. So, that we can establish all the required relations like:
\[\begin{align}
& \angle PAB+\angle QBA={{180}^{\circ }} \\
& \angle PAC+\angle QBC={{180}^{\circ }} \\
\end{align}\]
This relation plays a crucial role in proving that:
\[\begin{align}
& \angle AOB={{90}^{\circ }} \\
& \\
\end{align}\]
Complete step-by-step Solution:
Let us look at some of the basic definitions.
CIRCLE: Circle is defined as the locus of a point which moves in a plane such that its distance from a fixed point in that plane is constant.
TANGENT: In geometry, a tangent line to a circle is a line that touches the circle at exactly one point, never entering the circle's interior
CONGRUENCE OF TRIANGLES:
Two triangles that are identical in all respects are said to be congruent and are denoted by the symbol \[\cong \]. In two congruent triangles,
The corresponding sides are equal.
The corresponding angles are equal.
Conditions for two triangles to be congruent:
Three sides of one triangle are respectively equal to three sides of the second triangle (SSS).
Two sides and the included angle of one triangle respectively equal to two sides and the included angle of another triangle (SAS).
Two angles and the included side of one triangle are respectively equal to two angles and the included side of another triangle (ASA).
Two right angled triangles are congruent, if the hypotenuse and one side of one triangle are respectively equal to the hypotenuse and one side of another right angled triangle (RHS).
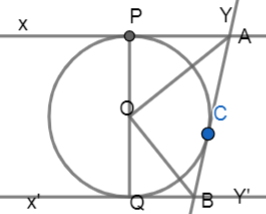
Now, let us look at the diagram clearly,

As we already know that tangent to a circle is perpendicular to the radius of circle at the point of contact.
\[OP\bot XY\]
\[OC\bot AB\]
In triangle OPA and OCA
\[\angle OPA=\angle OCA={{90}^{\circ }}\]
As they are tangents to the circle at points P and C.
\[OP=OC\]
As they are radii of the same circle.
\[AP=AC\]
We already know that lengths of the tangent from an external point are equal.
Now, by observing the above conditions from SAS congruence we can say that,
\[\therefore \vartriangle OPA\cong \vartriangle OCA\]
\[\therefore \angle OAP=\angle OAC\]
\[\therefore \angle OAC=\dfrac{1}{2}\angle PAC\]
Similarly, we can also say that.
\[\begin{align}
& \angle OBC=\angle OBQ \\
& \angle OBC=\dfrac{1}{2}\angle QBC \\
\end{align}\]
As we know that XY and X'Y' are parallel. So, here AB acts as a transversal.
We already know that sum of the interior angles on the same side of a transversal is
\[{{180}^{\circ }}\]
\[\angle PAB+\angle QBA={{180}^{\circ }}\]
Similarly, by considering the other part we get,
\[\angle PAC+\angle QBC={{180}^{\circ }}\]
On diving with 2 on both sides the above equation becomes:
\[\dfrac{1}{2}\left( \angle PAC+\angle QBC \right)={{90}^{\circ }}\]
\[\angle OAC+\angle OBC={{90}^{\circ }}\]
\[\left[ \because \angle OAC=\angle OAB,\angle OBC=\angle OBA \right]\]
From triangle OAB we can write,
\[\begin{align}
& \angle AOB+\angle OAB+\angle OBA={{180}^{\circ }} \\
& \angle AOB={{180}^{\circ }}-\left( \angle OAB+\angle OBA \right) \\
& \angle AOB={{180}^{\circ }}-{{90}^{\circ }} \\
& \therefore \angle AOB={{90}^{\circ }} \\
\end{align}\]
Note:
In order to prove the congruence you need to look at all the sides and angles which are equal because neglecting one of them changes the rule of congruence.
As we know that the line joining the centre and the external point from where tangents are drawn to the circle bisects the angle formed at the external point to the circle.
\[\angle OAP=\angle OAC\]
It is important to note that AB acts as a transversal to the parallel lines XY and X'Y'. So, that we can establish all the required relations like:
\[\begin{align}
& \angle PAB+\angle QBA={{180}^{\circ }} \\
& \angle PAC+\angle QBC={{180}^{\circ }} \\
\end{align}\]
This relation plays a crucial role in proving that:
\[\begin{align}
& \angle AOB={{90}^{\circ }} \\
& \\
\end{align}\]
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 8 Maths: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Which animal has three hearts class 11 biology CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Explain zero factorial class 11 maths CBSE

Mention the basic forces in nature class 11 physics CBSE

What is centripetal acceleration Derive the expression class 11 physics CBSE

Bond order ofO2 O2+ O2 and O22 is in order A O2 langle class 11 chemistry CBSE




