Question

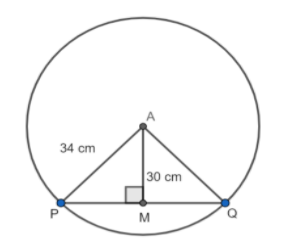
In fig. point A is a center of a circle AP = 34 cm, A is the center of a circle, AM = 30 cm. If \[AM\bot PQ\] , find the length of the chord PQ.

Answer 1

Hint: In the \[\Delta AMP\] , we have AM = Perpendicular = 30 cm, AP = Hypotenuse = 34 cm, PM = Base, and \[\angle AMP=90{}^\circ \] . Since the line segment, AM is perpendicular to the chord PQ so, we can apply the Pythagoras theorem in \[\Delta AMP\] . We know the Pythagoras theorem, \[{{\left( Hypotenuse \right)}^{2}}={{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}\] . Now, apply the Pythagoras theorem in the \[\Delta AMP\] and get the length of PM. We know the property that the perpendicular line drawn from the center to a chord of a circle bisects the chord. Here, AM is perpendicular to the chord PQ. So, the line AM bisects the chord PQ. M is the midpoint of the chord PQ. Therefore, \[PQ=2PM\] . Now, using the length of PM, get the length of PQ.

Complete step-by-step answer:
According to the question, we have a circle in which there is a chord PQ. The line segment AM drawn from the center A to the chord PQ such that AM is perpendicular to the chord PQ.

From the figure, we have
The length of the line segment AP = 34 cm …………………………………(1)
The length of the line segment AM = 30 cm …………………………………(2)
In the \[\Delta AMP\] , we have
AM = Perpendicular = 30 cm ………………………………………….(3)
AP = Hypotenuse = 34 cm …………………………………………..(4)
PM = Base ………………………………………(5)
\[\angle AMP=90{}^\circ \] ……………………………………….(6)
Since the line segment, AM is perpendicular to the chord PQ so, we can apply the Pythagoras theorem in \[\Delta AMP\] .
We know the Pythagoras theorem,
\[{{\left( Hypotenuse \right)}^{2}}={{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}\] ………………………………………………….(7)
Now, from equation (3), equation (4), equation (5), and equation (7), we have
\[\begin{align}
  & \Rightarrow {{\left( 34 \right)}^{2}}={{\left( 30 \right)}^{2}}+{{\left( PM \right)}^{2}} \\
 & \Rightarrow 1156=900+{{\left( PM \right)}^{2}} \\
 & \Rightarrow 1156-900={{\left( PM \right)}^{2}} \\
 & \Rightarrow 256={{\left( PM \right)}^{2}} \\
 & \Rightarrow \sqrt{256}=PM \\
 & \Rightarrow 16=PM \\
\end{align}\]
The length of the line segment PM is equal to 16 cm ……………………………….(8)
We know the property that the perpendicular line drawn from the center to a chord of a circle bisects the chord ……………………………………..(9)
Here, the line segment AM is also perpendicular to the chord PQ. Using the property shown in equation (9), we can say that the line AM bisects the chord PQ. It means that the point M is the midpoint of the chord PQ.
Since M is the midpoint of the chord PQ so,
\[PQ=2PM\] ……………………………………….(10)
 From equation (8), we have the length of the line segment PM.
Now, on substituting PM by 16 cm in equation (10), we get
\[PQ=2\left( 16\,cm \right)=32\,cm\]
Therefore, the length of the line segment PQ is equal to 32 cm.

Note: We can also solve this question without using the property that the perpendicular line drawn from the center to a chord of a circle bisects the chord.

In the \[\Delta AMP\] , we have
AM = Perpendicular = 30 cm ………………………………………….(1)
AP = Hypotenuse = 34 cm …………………………………………..(2)
PM = Base ………………………………………(3)
\[\angle AMP=90{}^\circ \] ……………………………………….(4)
Since the line segment, AM is perpendicular to the chord PQ so, we can apply the Pythagoras theorem in \[\Delta AMP\] .
We know the Pythagoras theorem,
\[{{\left( Hypotenuse \right)}^{2}}={{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}\] ………………………………………………….(5)
Now, from equation (1), equation (2), equation (3), and equation (5), we have
\[\begin{align}
  & \Rightarrow {{\left( 34 \right)}^{2}}={{\left( 30 \right)}^{2}}+{{\left( PM \right)}^{2}} \\
 & \Rightarrow 1156=900+{{\left( PM \right)}^{2}} \\
 & \Rightarrow 1156-900={{\left( PM \right)}^{2}} \\
 & \Rightarrow 256={{\left( PM \right)}^{2}} \\
 & \Rightarrow \sqrt{256}=PM \\
\end{align}\]
\[\Rightarrow 16=PM\] ……………………………………….(6)
We know the sum of the linear pair of angles is always \[180{}^\circ \] .
Since \[\angle AMP\] and \[\angle AMQ\] are linear pairs of angles so, the summation of the angles \[\angle AMP\] and \[\angle AMQ\] is \[180{}^\circ \] .
\[\angle AMP+\angle AMQ=180{}^\circ \] …………………………………………………(7)
Now, from equation (4) and equation (7), we get
\[\begin{align}
  & \Rightarrow 90{}^\circ +\angle AMQ=180{}^\circ \\
 & \Rightarrow \angle AMQ=180{}^\circ -90{}^\circ \\
 & \Rightarrow \angle AMQ=90{}^\circ \\
\end{align}\]
\[AP=AQ=16\,cm\] (radius of a circle is always equal)
Now, in the \[\Delta AMQ\] , we have
AM = Perpendicular = 30 cm ………………………………………….(8)
AQ = Hypotenuse = 34 cm …………………………………………..(9)
MQ = Base ………………………………………(10)
\[\angle AMQ=90{}^\circ \] ……………………………………….(11)
We know the Pythagoras theorem,
\[{{\left( Hypotenuse \right)}^{2}}={{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}\] ………………………………………………….(12)
Now, from equation (8), equation (9), equation (10), and equation (12), we have
\[\begin{align}
  & \Rightarrow {{\left( 34 \right)}^{2}}={{\left( 30 \right)}^{2}}+{{\left( MQ \right)}^{2}} \\
 & \Rightarrow 1156=900+{{\left( MQ \right)}^{2}} \\
 & \Rightarrow 1156-900={{\left( MQ \right)}^{2}} \\
 & \Rightarrow 256={{\left( MQ \right)}^{2}} \\
 & \Rightarrow \sqrt{256}=MQ \\
\end{align}\]
\[\Rightarrow 16=MQ\] ……………………………………….(13)
From the figure, we can see that
\[PQ=PM+MQ\] ………………………………………..(14)
Now, from equation (6), equation (13), and equation (14), we have
\[PQ=16\,cm+16\,cm=32\,cm\] .
Therefore, the length of the line segment PQ is equal to 32 cm.