Question

In $\Delta ABC$, $AB=8cm$, $AC=5cm$ and $\angle A=50{}^\circ $. Then
(a) What is the length of the perpendicular from $C$ to $AB$?
(b) Find the length of $BC$.
$[\sin 50{}^\circ =0.7660,\cos 50{}^\circ =0.6428,\tan 50{}^\circ =1.1918]$

Answer 1

Hint:We have to find the length of $CD$ and $BC$. For that consider $\Delta ACD$ and take $\sin A$. Then substitute the values, you will get $CD$. Now, for $BC$consider $\cos A$and find the value of $AD$. Prove the $\Delta ACD$ and $\Delta CDB$ congruent and then from that $AD=BD$. After that, consider $\Delta CDB$ and use pythagora's theorem to find length of $BC$. Try it, you will get the answer.

Complete step-by-step answer:
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices $A$, $B$, and $C$ is denoted $\Delta ABC$.

In Euclidean geometry, any three points, when non-collinear, determine a unique triangle and simultaneously, a unique plane (i.e. a two-dimensional Euclidean space). In other words, there is only one plane that contains that triangle, and every triangle is contained in some plane. If the entire geometry is only the Euclidean plane, there is only one plane and all triangles are contained in it; however, in higher-dimensional Euclidean spaces, this is no longer true. This article is about triangles in Euclidean geometry, and in particular, the Euclidean plane, except where otherwise noted.

The sum of the measures of the interior angles of a triangle in Euclidean space is always $180{}^\circ $. This fact is equivalent to Euclid's parallel postulate. This allows determination of the measure of the third angle of any triangle given the measure of two angles. An exterior angle of a triangle is an angle that is a linear pair (and hence supplementary) to an interior angle. The measure of an exterior angle of a triangle is equal to the sum of the measures of the two interior angles that are not adjacent to it; this is the exterior angle theorem. The sum of the measures of the three exterior angles (one for each vertex) of any triangle is $360{}^\circ $.

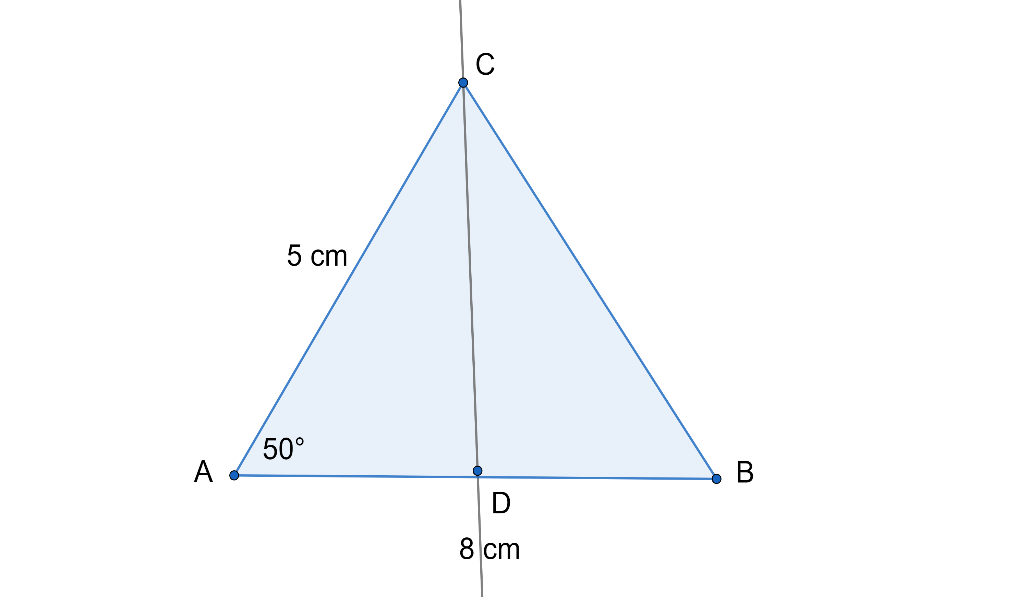
In the above figure, let $CD$ perpendicular to $AB$.
Now in $\Delta ACD$,
$\sin A=\dfrac{CD}{AC}$

Now, substituting the values we get,
$\sin 50{}^\circ =\dfrac{CD}{5}$
$\begin{align}
& CD=\sin 50{}^\circ \times 5 \\
& CD=0.7660\times 5 \\
\end{align}$
$CD=3.83cm$
Also,
$\cos A=\dfrac{AD}{AC}$
Now, substituting the values we get,
$\begin{align}
& \cos 50{}^\circ =\dfrac{AD}{5} \\
& \cos 50{}^\circ \times 5=AD \\
& AD=0.6428\times 5 \\
\end{align}$
$AD=4.786cm$

Now in right angle $\Delta ACD$,
$\angle A=50{}^\circ $ and $\angle CDA=90{}^\circ $
So $\angle C=180{}^\circ -(\angle A+\angle CDA)=180{}^\circ -(50{}^\circ +90{}^\circ )=180{}^\circ -140{}^\circ =40{}^\circ $
$\angle C=40{}^\circ $

Similarly, in $\Delta CDB$,
We get, $\angle B=40{}^\circ $
So in $\Delta ACD$ and $\Delta CDB$,
$\angle B=\angle C=40{}^\circ $ and $\angle CDA=\angle CDB=90{}^\circ $

Therefore, $\Delta ACD\cong \Delta CDB$ ………………….. (AA similarity)
Since, $\Delta ACD\cong \Delta CDB$
$AD=DB=4.786cm$

Now in right angle $\Delta CDB$,
by Pythagoras theorem,
$B{{C}^{2}}=C{{D}^{2}}+D{{B}^{2}}$

So substituting the values we get,
\[\begin{align}
& B{{C}^{2}}={{(3.83)}^{2}}+{{(4.786)}^{2}} \\
& B{{C}^{2}}=14.61+22.61 \\
& B{{C}^{2}}=37.58 \\
\end{align}\]
$BC=\sqrt{37.58}cm$

Therefore, we get the length of perpendicular $CD$ and length of $BC$as $3.83cm$ and $\sqrt{37.58}cm$ respectively.

Note: Read the question in a careful manner. Also you must know the basic concepts related to triangles and its properties. Do not make any silly mistakes. Also, take care that while simplifying no confusion occurs. Don’t jumble yourself while simplifying the problem.