Question

In any triangle ABC, if the angle bisector $\angle A$ and perpendicular of BC intersect, prove that they intersect on the circumcircle of triangle ABC.

Answer 1

Hint:We will try to establish a relation between angle subtended by BD on centre of circle and angle subtended at any other point on circle then we use the property of chords to get the final result. Properties of triangles will also be used.
The following is the schematic diagram of the triangle ABC inscribed in a circle having centre O.

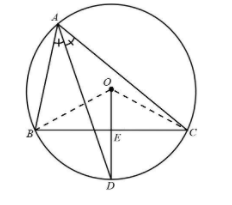
 Complete step-by-step solution
Construction
Draw the circle through the points A, B and P and Join line OB and OC.
Since, BC is a chord so its perpendicular bisector will pass through centre O of the circumcircle.
As, angle subtended by an arc on the centre is double then the angle subtended at any other point on the circle will be,
$\angle BOC = 2\angle BAC$ ……….(1)
In triangle BOE and triangle COE, the OD bisects chord BC, both the right angles are equal because OD is perpendicular to BC and OE is a common line in both the triangles.
$\begin{array}{c}
BE = CE\;\\
\angle BEO = \angle CEO\\
OE = OE
\end{array}$
The both triangles $\Delta BOE \cong \Delta COE$ are congruent because of SAS congruency rule.
Also, by the help of CPCT,
$\angle BOE = \angle COE\;$
Now, we know that
$\angle BOC = \angle BOE + \angle COE$

Since, angle $\angle BOE = \angle COE\;$then the above relation will become,
$\angle BOC = 2\angle BOE$ ……(2)
Also, AD is bisector of angle A.
$\angle BAC = 2\angle BAD$ …. (3)
From equations (1) and (2), we can say that
$\angle BAC = \angle BOE$
Substituting the $\angle BOE$ in equation (3) we get,
$\angle BOE = 2\angle BAD$
Now, BD subtends angle BOE at centre and half of its angle at point A. So, BD must be a chord.
Therefore, D lies on a circle and it is proving that they intersect on the circumcircle of the triangle ABC.

Note:Circumcircle of a triangle is a circle on which all three vertices of triangle lie. Make sure to draw the circle through the points A, B and P and join line OB and OC.