Question

In an isosceles triangle \[ABC\left( {AB = AC} \right)\], the altitude to the base and to the lateral side are equal to 10 cm and 12 cm respectively. The length of the base is
A. 12.5
B. 15
C. 16
D. 18

Answer 1

Hint: In this question, we will be using the formula of half-angles in trigonometry and using the sides of the triangle we will obtain the unknown sides. Also, we will use the property of altitude to the base in case of isosceles triangle to get the required solution. So, use this concept to reach the solution of the given problem.

Complete step by step answer:
Given \[\Delta ABC\] is an isosceles triangle with \[AB = AC\]. Let \[AD\] be the altitude to the base and \[CE\] be the altitude to the lateral side whose length are equal to 10 cm and 12 cm respectively as shown in the below figure:

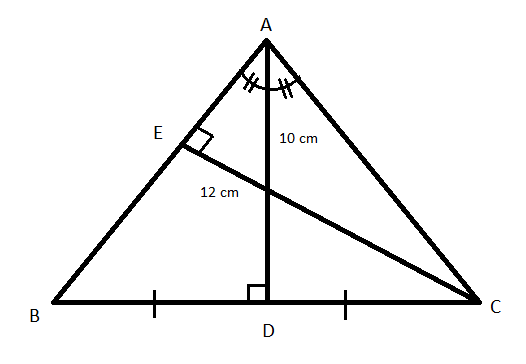
By applying \[\sin B\] in \[\Delta ABD\] and \[\Delta BCE\], we get
\[
   \Rightarrow \sin B = \dfrac{{AD}}{{AB}} = \dfrac{{CE}}{{BC}} \\
   \Rightarrow \sin B = \dfrac{{10}}{{AB}} = \dfrac{{12}}{{BC}} \\
   \Rightarrow \dfrac{{10}}{{AB}} = \dfrac{{12}}{{BC}} \\
   \Rightarrow BC = \dfrac{{12}}{{10}}AB \\
  \therefore BC = 1.2AB \\
\]
We know that the altitude to the base divides the angle at where the two equal side lengths meet into two equal angles.
So, \[\angle BAC = \dfrac{1}{2}\angle BAD = \dfrac{1}{2}\angle DAC\]
We know that altitude to the base in an isosceles triangle divides the base in two equal parts.
So, we have \[BC = 2BD = 2DC\]
Now in \[\Delta ABD\] we have
\[
   \Rightarrow \sin \dfrac{A}{2} = \dfrac{{BD}}{{AB}} = \dfrac{{\dfrac{{BC}}{2}}}{{AB}} = \dfrac{{\dfrac{{1.2AB}}{2}}}{{AB}} = 0.6{\text{ }}\left[ {\because BC = 1.2AB} \right] \\
   \Rightarrow \cos \dfrac{A}{2}{\text{ = }}\sqrt {1 - {{\left( {0.6} \right)}^2}} = 0.8{\text{ }}\left[ {\because \cos \dfrac{A}{2} = \sqrt {1 - {{\sin }^2}\dfrac{A}{2}} } \right] \\
   \Rightarrow \tan \dfrac{A}{2}{\text{ = }}\dfrac{{BD}}{{AD}} = \dfrac{{\sin \dfrac{A}{2}}}{{\cos \dfrac{A}{2}}} = \dfrac{{0.6}}{{0.8}} = \dfrac{3}{4} = 0.75 \\
  \therefore \dfrac{{BD}}{{AD}} = 0.75 \Rightarrow BD = 10 \times 0.75 = 7.5{\text{ }}\left[ {\because AD = 10} \right] \\
\]
We know that altitude to the base in an isosceles triangle divides the base in two equal parts.
So, \[BC = 2 \times BD = 2 \times 7.5 = 15\]
Therefore, the length of the base is \[BC = 15{\text{cm}}\]

So, the correct answer is “Option B”.

Note: We have to use a trigonometric formula to solve this question. The formula used is \[\cos \dfrac{A}{2} = \sqrt {1 - {{\sin }^2}\dfrac{A}{2}} \]. Also, we have to use \[\sin A = \dfrac{{{\text{opp side}}}}{{{\text{hypotenuse}}}}\] and \[\tan \dfrac{A}{2} = \dfrac{{\sin \dfrac{A}{2}}}{{\cos \dfrac{A}{2}}}\]. Also, we should remember the property of the isosceles triangle that opposite sides are always equal and opposite angles are also equal.