Question

In an astronomical telescope in normal adjustment a straight black line of length $L$ is drawn on the inside part of the objective lens. The eye-piece forms a real image of this line. The length of this image is $l$. The magnification of the telescope is:

A.)$\dfrac{L}{l}$
B.)$\dfrac{L}{l} + 1$
C.)$\dfrac{L}{l} - 1$
D.)$\dfrac{L+l}{L-l}$

Answer 1

Hint: Try to recall what normal adjustment is. In other words, when a telescope is set to normal adjustment the object distance becomes the sum of the focal lengths of the objective lens and the eye-piece. Substituting this in the lens formula should get you going.

Formula used:
Lens formula: $\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u} $ where $f$ is the focal length, $u$ is the object distance and $v$ is the image distance.
Magnification $M = \dfrac{Image\; height}{Object\;height}$ or $M = -\;\dfrac{v}{u}$.
Object distance $u = - (f_0 +f_e)$ where $f_0$ is the focal length of the objective lens and $f_e$ is the focal length of the eye-piece (applicable only here).

Complete step-by-step answer:
Let us deconstruct the question and understand what it means.
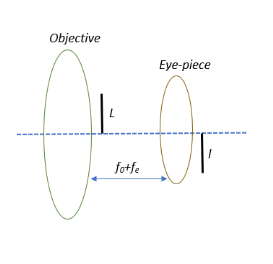
So, we have an astronomical telescope and we draw a straight line on the inside part of the objective lens. This line becomes the object for the eye-piece.
Now let us understand what normal adjustment is. When a telescope is adjusted so that the final image of a distant object is at infinity so that the eye is completely relaxed while viewing it is called normal adjustment. This is achieved when the distance between the objective and the eyepiece is equal to their focal lengths added together. The image formed by the objective lens will now lie between the principal focus and the optical centre of the eye lens instead of laying at the focus of the eye lens. This creates a virtual image at a finite distance from the eye lens.
From the diagram we can deduce that the object distance $u = - (f_0 +f_e)$. The negative sign is a convention for the object distance of all lenses and mirrors.

Substituting the object distance in the lens formula with respect to the eyepiece:

$\dfrac{1}{f} = \dfrac{1}{v} -\dfrac{1}{u} \Rightarrow \dfrac{1}{f_e} = \dfrac{1}{v} - \dfrac{1}{- (f_0 +f_e)} \Rightarrow \dfrac{1}{v} = \dfrac{1}{f_e} - \dfrac{1}{(f_0 +f_e)}$
$\Rightarrow \dfrac{1}{v} = \dfrac{f_0+f_e-f_e}{f_e(f_0+f_e)} \Rightarrow \dfrac{1}{v} = \dfrac{f_0}{f_e(f_0+f_e)} \Rightarrow v = \dfrac{ f_e(f_0+f_e)}{f_0} $

We know that magnification $M = \dfrac{Image\; height}{Object\;height}$ or $M = -\;\dfrac{v}{u}$. Equating the two and substituting line lengths:

$ -\dfrac{v}{u} = \dfrac{Image\; height}{Object\;height} \Rightarrow \dfrac{l}{L} = -\; \dfrac{\dfrac{ f_e(f_0+f_e)}{f_0}}{- (f_0 +f_e)} = \dfrac{f_e(f_0+f_e)}{f_0(f_0+f_e)} $
$\Rightarrow \dfrac{l}{L} = \dfrac{f_e}{f_0}$

But in normal adjustment, magnification is given as $M = \dfrac{f_0}{f_e} = \dfrac{L}{l}$

So, the correct answer is “Option A”.

Note:
Keep in mind that in accordance with the Cartesian sign convention, the object distances (u) are always negative since the object is placed to the left of the lens.
Also remember that for a telescope to be in normal adjustment the distance between the objective and the eyepiece should be equal to their focal lengths added together. Unless specified, you cannot assume the normal adjustment condition for all cases.