Question

In a YDSE bichromatic light of wavelength 400nm and 560nm are used. The distance between the slits is 0.1mm and the distance between the plane of the slits and screen is 1.0m. The minimum distance between two successive regions of complete darkness is
1) 4mm
2) 5.6mm
3) 14mm
4) 28mm

Answer 1

Hint: First consider that ${{n}^{th}}$ minima of first wavelength coincides with ${{m}^{th}}$ minima of second wavelength. Then equate both the equations. Then find the value of m and n in two cases considering two ratios. Then the location of minima is calculated using both the values of m and n. Thus the minimum distance between two successive regions is the difference of those two distances.
Formula used:
$\dfrac{(2n-1){{\lambda }_{1}}D}{2d}=\dfrac{(2m-1){{\lambda }_{2}}D}{2d}$
where, d is the distance between the slits.
D , the distance between the slit and screen.
${{\lambda }_{1}}\And {{\lambda }_{2}}$ are the wavelengths of light used.
m and n are the order of interference.

Complete answer:

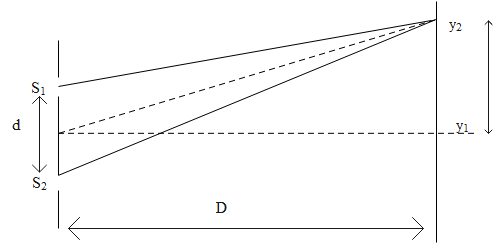
Let ${{n}^{th}}$ minima of 400nm coincides with ${{m}^{th}}$ minima then,
$\dfrac{(2n-1){{\lambda }_{1}}D}{2d}=\dfrac{(2m-1){{\lambda }_{2}}D}{2d}$
$\Rightarrow $ (2n-1)$\times 400=(2m-1)\times 560$
 $\dfrac{2n-1}{2m-1}=\dfrac{560}{400}=\dfrac{28}{20}=\dfrac{14}{10}=\dfrac{7}{5}$ =$\dfrac{21}{15}$
If we the ratio $\dfrac{7}{5}$, n=4 and m=3. Then take the second ratio $\dfrac{14}{10}$ , then n=7.5 and m=5.5. This is not acceptable. So consider the next ratio $\dfrac{21}{15}$ , n=11 and m= 8.
That is ${{4}^{th}}$ minima of 400nm coincides with the ${{3}^{rd}}$ minima of 560nm.Then the location of minima is,
${{y}_{1}}=\dfrac{(2\times 4-1)\times 400\times {{10}^{-6}}\times 1000}{2\times 0.1}=14mm$
Similarly ${{11}^{th}}$ minima of 400nm coincides with ${{8}^{th}}$ minima of 560nm. Then the location of minima is,
${{y}_{2}}=\dfrac{(2\times 8-1)(560\times {{10}^{-6}})\times 1000}{2\times 0.1}=42mm$
Therefore the required distance is,
${{y}_{2}}-{{y}_{_{1}}}=42-14=28mm$

Then the option(4) is correct.

Additional information:
To obtain constructive interference for a double slit, the path length difference must be an integral multiple of the wavelength.
$d\sin \theta =m\lambda $
 For m= 0,1,-1,2,-2,…… (Constructive interference)
$d\sin \theta =\left( m+\dfrac{1}{2} \right)\lambda $
For m=0,1,-1,2,-2,……….(Destructive interference)
Here, $\lambda $ is the wavelength of light, d is the distance between the slits and m is the order of interference.

Note:
The value of m and n should not be a decimal or a fractional number. While calculating the value of m and n if we are getting a fractional or decimal number then we should take another set of ratios and we should find the values of m and n. Then by taking two values of m and n we can find the location of minima and the required distance is their difference.