Question

In a survey of \[60\] people, it was found that \[25\] people read newspaper \[H\], \[26\] read newspaper \[T\], \[26\] read newspaper \[I\], \[9\] read both \[H\] and \[I\], \[11\] read both \[H\] and \[T\], \[8\] read both \[T\] and \[I\], \[3\] read all the three newspapers. Find:
(i) The number of people who read at least one of the newspapers
(ii) The number of people who read exactly one newspaper.

Answer 1

Hint: Assume the variables representing the number of people who read different kinds of newspapers. Solve them to get the exact count of people who read each kind of newspaper. To count the number of people who read at least one of the newspapers, one should count the total number of people reading one, two or three newspapers. To count the number of people who read exactly one newspaper, one should sum up the number of people reading only one newspaper, for all the three newspapers.

Complete step-by-step answer:
We have data regarding the count of people who read different newspapers. We have to evaluate the number of people who read at least one of the newspapers and the number of people who read exactly one newspaper.
We will solve this by creating a venn diagram and using variables to represent the number of people who read different kinds of newspaper.

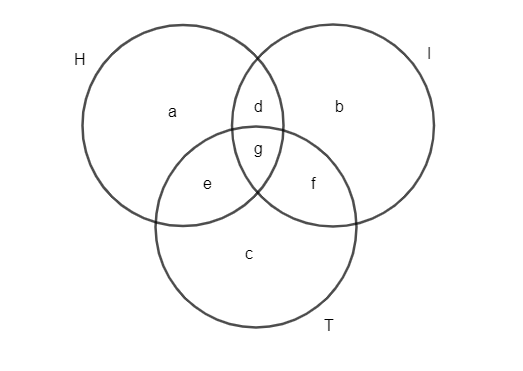
Let’s assume \[a\] number of people read only newspaper \[H\], \[b\] number of people read only newspaper \[I\], \[c\] number of people read only newspaper \[T\], \[d\] number of people read both newspapers \[H\] and \[I\], \[e\] number of people read both newspapers \[H\] and \[T\], \[f\] number of people read both newspapers \[I\] and \[T\] while \[g\] number of people read all the three newspapers.
We know that \[25\] people read newspapers \[H\]. So, we have \[a+d+e+g=25.....\left( 1 \right)\].
We know that \[26\] people read newspapers \[I\]. So, we have \[b+d+f+g=26.....\left( 2 \right)\].
We know that \[26\] people read newspapers \[T\]. So, we have \[c+e+f+g=26.....\left( 3 \right)\].
We know that \[9\] people read both \[H\] and \[I\]. So, we have \[d+g=9.....\left( 4 \right)\].
We know that \[11\] people read both \[H\] and \[T\]. So, we have \[e+g=11.....\left( 5 \right)\].
We know that \[8\] people read both \[T\] and \[I\]. So, we have \[f+g=8.....\left( 6 \right)\].
As three people read all the newspapers, we have \[g=3\].
Substituting the value \[g=3\] in equation \[\left( 6 \right)\], we have \[f+3=8\Rightarrow f=5\].
Substituting the value \[g=3\] in equation \[\left( 5 \right)\], we have \[e+3=11\Rightarrow e=8\].
Substituting the value \[g=3\] in equation \[\left( 4 \right)\], we have \[d+3=9\Rightarrow d=6\].
Substituting the above calculated values in equation \[\left( 1 \right)\], we have \[a+6+8+3=25\Rightarrow a=8\].
Substituting the above calculated values in equation \[\left( 2 \right)\], we have \[b+6+5+3=26\Rightarrow b=12\]. Substituting the above calculated values in equation \[\left( 3 \right)\], we have \[c+8+5+3=26\Rightarrow c=10\].
We have calculated the value of each of the parameters now.
We will find the values asked in the question.
(i) We have to calculate the number of people who read at least one of the newspapers. So, we will consider all the people who read one, two and three newspapers.
Number of people who read only one newspaper \[=a+b+c=8+12+10=30\].
Number of people who read two newspapers \[=d+e+f=6+8+5=19\].
Number of people who read three newspapers \[=g=3\].
So, the total number of people who read at least one newspaper \[=30+19+3=52\].
Hence, \[52\] people read at least one newspaper according to the given data.
(ii) We have to calculate the number of people who read exactly one newspaper.
 Number of people who read one newspaper \[=a+b+c=8+12+10=30\].
Hence, \[30\] people read only one newspaper.

Note: It’s necessary to draw venn diagrams to write equations to solve this question. Otherwise, we won’t be able to get a correct answer. One needs to understand how the number of people reading different newspapers is distributed.