Question

In a survey of 100 persons it was found that 28 read magazines A, 30 read magazines B, 42 read magazines C, 8 read magazines A and B, 10 read magazines A and C, 5 read magazines B and C and 3 read all the three magazines. Find the number of persons who read:
A. A only
B. B only
C. C only
D. A and B but not C
E. B and C but not A
F. A and C but not B
G. Exactly one of the magazines
H. At least one of the three magazines
I. None of the three magazines

Answer 1

Hint: To find the given data, let us first draw the Venn diagram. The required solutions can be obtained clearly from this. The only section you will have to be careful of is when assigning the data in the Venn Diagram.

Complete step-by-step solution
Let us write the given data and draw the Venn diagram in the following manner to find the required number of people.
Let the total number of people be n(U) =100
Let us denote the number of persons who read magazine A to be n(A)=28
Let the number of persons who read magazine B be n(B)=30
Let us denote the number of persons who read magazine C as n(C)=42
It is also given that the number of people who read both the magazine A and B, denoted as \[n(A\cap B)=8\]
Let the number of people who read both A and C be \[n(A\cap C)=10\]
The number of people who read both B and C is given as \[n(B\cap C)=5\]
The number of people who read all the three magazines is denoted as \[n(A\cap B\cap C)=3\]
Now, let us find the answers for each section from the Venn Diagram.

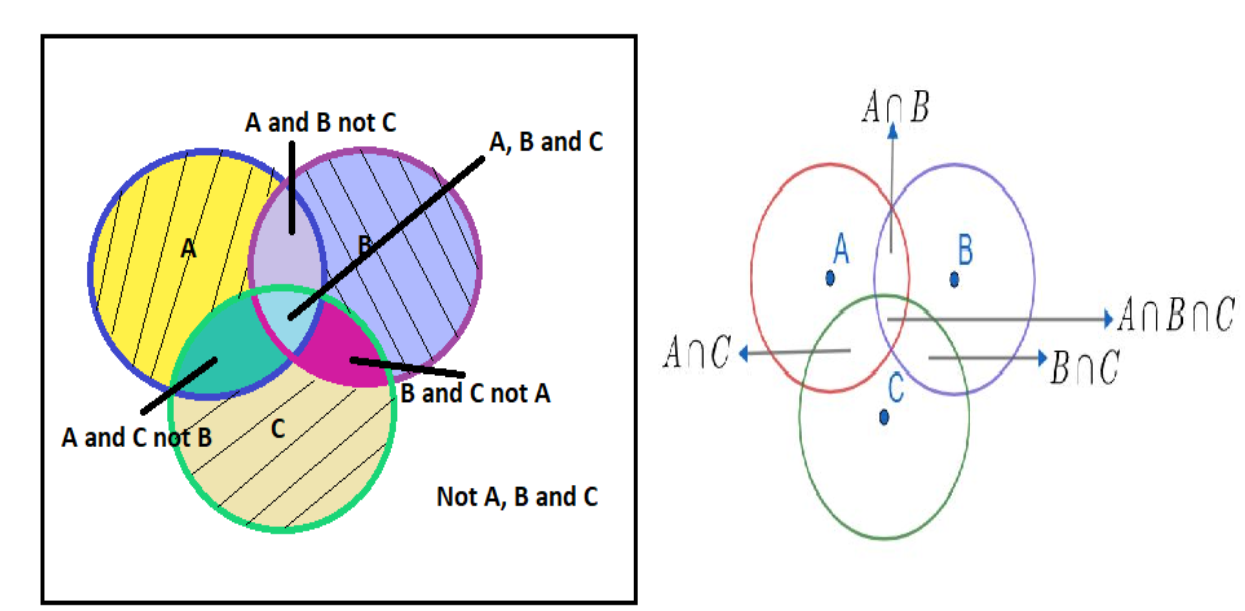
A). We have to find the number of people that read only magazine A, that is shown as a yellow shaded portion.
$=n(A)-n\text{(A and B not C)}-n\text{(A and C not B)}-n(A\cap B\cap C)$
$=n(A)-n(A\cap B\cap C')-n(A\cap C\cap B')-n(A\cap B\cap C)...(i)$
Let us solve this later as in the coming sections we will come across the solutions for $n(A\cap B\cap C')\text{ and }n(A\cap C\cap B')$

B. We have to find the number of people that read the only magazine B. This is given as a violet shaded region on the Venn diagram.
$=n(B)-n(A\cap B\cap C')-n(B\cap C\cap A')-n(A\cap B\cap C)...(ii)$
We will solve this later.
C. The number of people that read-only magazine C is shown as a brown shaded region in the Venn Diagram and is found as
$=n(C)-n(A\cap C\cap B')-n(B\cap C\cap A')-n(A\cap B\cap C)...(iii)$
This also, we will solve later.
D. The people who read A and B but not C (purple region) is given as
\[n(A\cap B\cap C')=n(A\cap B)-n(A\cap B\cap C)\]
$=8-3=5$
E. The people who read B and C but not A (pink region) is
\[n(B\cap C\cap A')=n(B\cap C)-n(A\cap B\cap C)\]
$=5-3=2$
F. The people who read A and C but not B (green region) is
\[n(A\cap C\cap B')=n(A\cap C)-n(A\cap B\cap C)\]
$=10-3=7$
Now, let us go back to section A.
Substituting the values from above, we get
The number of people that read only magazine A, that is shown as a yellow shaded portion.
$\begin{align}
  & =n(A)-n(A\cap B\cap C')-n(A\cap C\cap B')-n(A\cap B\cap C) \\
 & =28-5-7-3 \\
 & =13 \\
\end{align}$
Now, we will move on to section B.
The number of people that read only magazine B is given as
$\begin{align}
  & =n(B)-n(A\cap B\cap C')-n(B\cap C\cap A')-n(A\cap B\cap C) \\
 & =30-5-2-3 \\
 & =20 \\
\end{align}$
Let us move to section C.
The number of people that read only magazine C is given by
$\begin{align}
  & =n(C)-n(A\cap C\cap B')-n(B\cap C\cap A')-n(A\cap B\cap C) \\
 & =42-7-2-3 \\
 & =30 \\
\end{align}$
G. To find the number of people who read exactly one magazine, we will add the number of people reading only A, only B, and only C. That is,
$=13+20+36=69$
H. We have to find the number of people reading at least one of the three magazines. That is, the number of people reading one or more magazines. This is given as
$\begin{align}
  & n(A\cup B\cup C) \\
 & =\text{n(only A)+n(only B)+n(only C)+n(A and B not C)+n(A and C not B)+n(B and C not A)+n(A and B and C)} \\
 & =13+20+30+5+7+2+3 \\
 & =80 \\
\end{align}$
I. We need to find the number of people who do not read any of the three magazines.
We have to find the number of people reading at least one magazine to be 80.
The total number of people in the survey is given as 100.
Hence, people who do not read any of the magazines $=100-80=20$

Note: We can also solve this problem using formulas of sets. For example, $n(A\cup B\cup C)=n(A)+n(B)+n(C)-n(A\cap B)-n(B\cap C)-n(A\cap C)+n(A\cap B\cap C)$. The Venn Diagram must be drawn correctly, else the entire solution will be wrong. Here the term only means it does not include any elements of other sets.