Question

In a meter bridge experiment, the null point is obtained at 20 cm from one end of the wire when resistance X is balanced against another resistance Y. If X is less than Y, then where will the new position of the null point be from the same end, if one decides to balance a resistance of 4X against Y?
A. 40 cm
B. 80 cm
C. 50 cm
D. 70 cm

Answer 1

Hint: Find the relation between X and Y with the formula $\dfrac{X}{Y}=\dfrac{l}{100-l}$, where l is balanced from X. Then with this relation, find the new balanced length when the resistance X is replaced with 4X.

Formula used:
$\dfrac{X}{Y}=\dfrac{l}{100-l}$

Complete step-by-step answer:
Let us first understand the application of a meter bridge. A meter bridge is a device to find the relation between two unknown resistances or to find the value of an unknown resistance with help of a known resistance. It works on the principle of Wheatstone bridge. The device has a wire, one meter long with uniform resistance and to slots to attach the two resistances. It has a jockey with one end attached to the junction of the two resistances. The other end is used to balance the bridge.
A diagram of a meter bridge is given below.

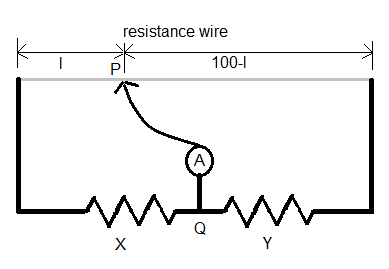
When the ammeter reads zero current, the bridge is balanced. We also call this a null point. Ats this point, the relation between the two resistances is given as:
$\dfrac{X}{Y}=\dfrac{l}{100-l}$, where X and Y are the values of the resistances.
Now, in the question, it is given that l=20cm.
Therefore, $\dfrac{X}{Y}=\dfrac{20}{100-20}=\dfrac{20}{80}=\dfrac{1}{4}$.
$\Rightarrow 4X=Y$.
The second case consists of resistances of 4X and Y. Let 4X=R and Y=S.
Hence, $\dfrac{R}{S}=\dfrac{l}{100-l}$
$\Rightarrow \dfrac{R}{S}=\dfrac{4X}{Y}=\dfrac{l}{100-l}$.
But we know that Y=4X.
Therefore,
$\dfrac{4X}{4X}=\dfrac{l}{100-l}$
$\Rightarrow 1=\dfrac{l}{100-l}$.
This implies that l=50 cm.
Therefore, when the resistance X is replaced with 4X, the new null point is obtained at a position of 50 cm from the end that has resistance 4X.
Hence, the correct option is C.

Note: The reason that we get a null point or zero current across P and Q is that the potential difference across P and Q is zero.
Please note that relation XY, then the position of the null point will also change. The smaller length is always in parallel with the resistance that has smaller value.