Question

In a Kundt’s tube experiment, the heaps of lycopodium powder are collected at 20cm separations. What will be the frequency of the tuning fork used?
\[\begin{align}
  & A.\text{ 660Hz} \\
 & \text{B}\text{. 825Hz} \\
 & \text{C}\text{. 775Hz} \\
 & \text{D}\text{. 915Hz} \\
\end{align}\]

Answer 1

Hint: The Kundt’s tube experiment is the acoustic experiment which describes the longitudinal wave pattern in the sound waves. The separation of piles formed by the given sample is a direct indicator of the characteristics of the sound wave used. The speed of sound in air is 340\[m{{s}^{-1}}\].
Formula Used:
The basic formula used in a Kundt’s experiment is –
\[c=\lambda \nu \]
Where, c is the speed of sound in vacuum or air
\[\lambda \] is the wavelength of the sound
\[\nu \] is the frequency of the sound

Complete answer:
The Kundt’s tube experiment consists of a transparent horizontal tube with a small amount of the given sample, here it is the lycopodium. The one end of the tube has a single signal generator which can produce a sound wave of single frequency \[\nu \]. The other end of the tube is attached with a movable piston which can oscillate along with the incoming sound wave and thus contributes to the length of the tube. The piston is set up such that the sound produced by the generator doesn’t disturb its equilibrium position at lower amplitudes. This means that the length of the tube along with the piston is a multiple of the wavelength of the generated sound.
The given figures give the amplitude variation at two instincts.

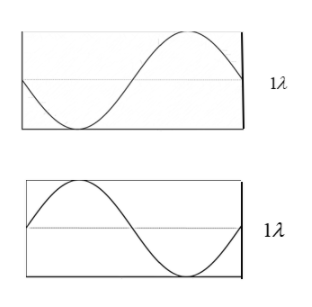
It is clear that the piston will be at equilibrium if \[L=n\lambda \].
Also, we know from the experiment that the powder used has a tendency to pile at distance half of the wavelengths.
Now using this idea and given data, we can find the frequency of the sound used.
\[\begin{align}
  & \text{Given}, \\
 & \text{ }\delta =20cm \\
 & \text{Also}, \\
 & \text{ }\dfrac{\lambda }{2}=\delta \\
 & \Rightarrow \dfrac{\lambda }{2}=20cm \\
 & \Rightarrow \lambda =40cm\text{ --------(1)} \\
\end{align}\]
Now, using the basic formula relating speed, wavelength and frequency we can find the frequency of the sound.
 \[\begin{align}
  & c=\lambda \nu \text{ -------(2)} \\
 & \text{From (1),} \\
 & \lambda =40cm=0.4m \\
 & \text{Also,} \\
 & c=340m{{s}^{-1}} \\
 & \Rightarrow \text{From (2),} \\
 & \text{ }\nu =\dfrac{c}{\lambda } \\
 & \Rightarrow \nu =\dfrac{340}{0.4} \\
 & \Rightarrow \nu =850Hz \\
\end{align}\]
The frequency with which the experiment was conducted is 850Hz.

Option B is the suitable answer.

Note:
In an experiment, the unknown we usually find is the wavelength of the generated sound wave. We find it similarly by measuring the distance between the piles of the lycopodium powder and applying the basic formula relating wavelength, frequency and speed of sound in the medium.
The experiment is also a proof for the longitudinal nature of the sound waves.