
In a
A.
B.
C.
D. None
Answer
516.6k+ views
Hint: The radius of a triangle is equal to
Complete step-by-step answer:
Given triangle ABC is right angled at B.
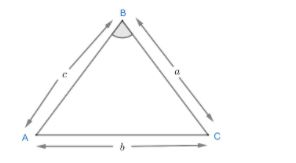
Now, let us put calculated values of
Multiplying both numerator and denominator by 2, we will get,
Putting AB = c, BC = a and AC = b, we will get;
Subtracting equation (1) from equation (2), we will get,
Taking LCM and subtracting, we will get,
We know
Using these identity, we will get,
Taking “-1” common, we will get,
As
By replacing
Multiplying both sides of equation by “-1”, we will get,
Taking “2b” common from the numerator in RHS, we will get,
Dividing both numerator and denominator by 2(a + b + c), we will get,
Putting
Taking LCM and subtracting, we will get,
Now, putting a = BC, b = AC, c = AB, we will get,
Hence, the inradius of
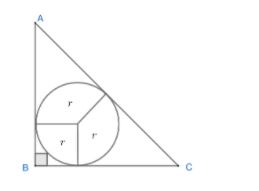
Note: inradius of a triangle is the radius of the circle inscribed in the triangle. If you don’t remember the formula for inradius. Calculate inradius using geometry. But this will be a very lengthy method, so try to memorize the formula.
Complete step-by-step answer:
Given triangle ABC is right angled at B.

Now, let us put calculated values of
Multiplying both numerator and denominator by 2, we will get,
Putting AB = c, BC = a and AC = b, we will get;
Subtracting equation (1) from equation (2), we will get,
Taking LCM and subtracting, we will get,
We know
Using these identity, we will get,
Taking “-1” common, we will get,
As
By replacing
Multiplying both sides of equation by “-1”, we will get,
Taking “2b” common from the numerator in RHS, we will get,
Dividing both numerator and denominator by 2(a + b + c), we will get,
Putting
Taking LCM and subtracting, we will get,
Now, putting a = BC, b = AC, c = AB, we will get,
Hence, the inradius of

Note: inradius of a triangle is the radius of the circle inscribed in the triangle. If you don’t remember the formula for inradius. Calculate inradius using geometry. But this will be a very lengthy method, so try to memorize the formula.
Recently Updated Pages
10 Best Commerce Colleges in India

Benefits of Participating in SOF Olympiad 2023-24

Personalized Tuition for IGCSE Biology: Proven Results for 2025

1-on-1 Online Tuition for IELTS, SAT & International Tests 2025

Low Rank in JEE Main 2020? Try in These Engineering Colleges

Class 4 Maths Mixed Numbers to Improper Fractions Worksheet PDF

Trending doubts
Choose the correct meaning of the given phrase To drive class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

Indias first jute mill was established in 1854 in A class 10 social science CBSE

Fill in the blank with the appropriate form of the class 10 english CBSE

Choose the correct meaning of the given phrase To drive class 10 english CBSE

Five things I will do to build a great India class 10 english CBSE




