Question

In a class of 100 students, 60 students drink tea 50 students drink coffee, and 30 students drink both. A student from this class is selected at random, finding the probability that student takes at least one of the two drinks.

Answer 1

Hint: Student taking at least one of the drinks means we need to find the probability of the student taking either one or both the drinks. As we have three values corresponding to three events, the formula connecting those is the probability union formula from which we will obtain the result.
* Indicating the given information as a Venn diagram and denoting each event as a letter, makes solving simpler.
* Probability of an event =Number of favourable event/Total event
* For two events A and B probability of happening of event A or event B, $P(A \cup B) = P(A) + P(B) - P(A \cap B)$

Complete step-by-step answer:
Venn diagram corresponding to the given information is as follows:
          

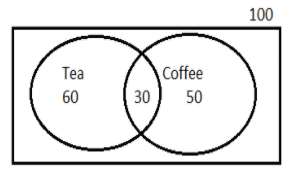
Let T denote people drinking tea, C denote coffee and the overlapping region shows people on both events.
We know Probability of an event is the number of favourable outcomes divided by the total number of outcomes.
Representing given information in probability form:
Probability of people drinking tea,
$
  P(T) = \dfrac{{60}}{{100}} \\
   = 0.6 \\
 $
Probability of people drinking coffee,
$
  P(C) = \dfrac{{50}}{{100}} \\
   = 0.5 \\
 $
Probability of people drinking both tea and coffee,
$
  P(T \cap C) = \dfrac{{30}}{{100}} \\
   = 0.3 \\
 $
Probability of student taking at least one of 2 drinks means either tea or coffee or both which is represented by its union,
$
  P(T \cup C) = P(T) + P(C) - P(T \cap C) \\
   = 0.6 + 0.5 - 0.3 \\
   = 0.8 \\
 $
Final answer:
Probability of students taking at least one of the two drinks = 0.8

Additional Information: Probability formula for union of three events is:
$P(A \cup B \cup C) = P(A) + P(B) + P(C) - P(A \cap B) - P(A \cap B) - P(A \cap C) - P(B \cap C) + P(A \cap B \cap C)$A hidden assumption in the above formula is these events are mutually exclusive.
This probability formula of union of events can be rearranged to find a solution for similar questions asking the intersection of events. Generalization of events to three and more can be used correspondingly

Note: Students mostly make the mistake of assuming the meaning of at least as either tea or coffee but it also includes people consuming both tea and coffee as well so we find the value of union.