Question

If two vertices of an equilateral triangle are $\left( 0,0 \right),\left( 3,\sqrt{3} \right)$ , find the third vertices of the triangle.

Answer 1

Hint: In equilateral triangle all angles are $\dfrac{\pi }{3}$ and length of all 3 sides are the same. In equilateral triangle altitudes and medians are the same for all sides. If we rotate point B with respect to point A by $\dfrac{\pi }{3}$ clockwise and anti-clockwise we will get C and D. We can use complex numbers to solve this question. Another method is to use coordinate geometry, first we will find the midpoint of AB then the equation of altitude through AB. We know that the third point will lie on that altitude at distance of height of the triangle.

Complete step-by-step solution:

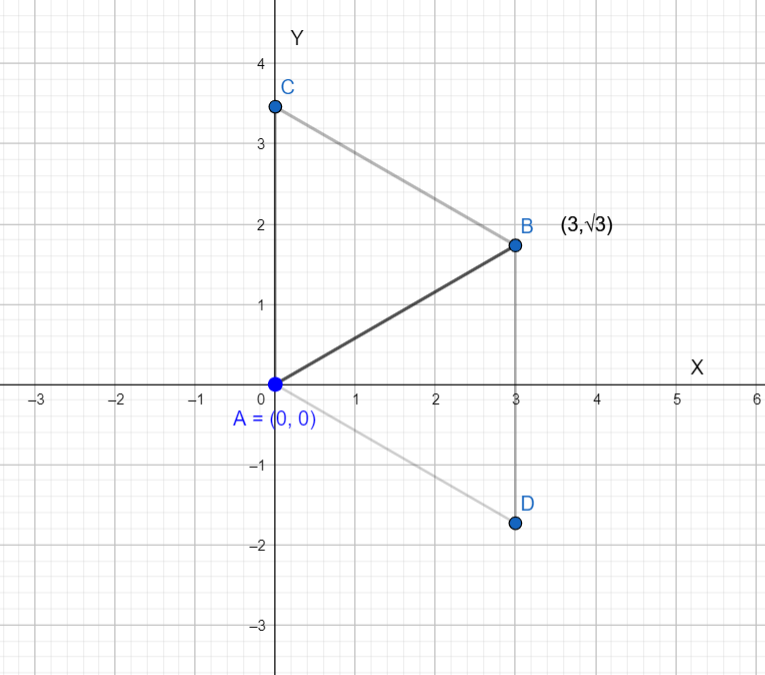
2 points of an equilateral triangle are given as A and B Shown in the above graph.
A= $\left( 0,0 \right)$ and B=$\left( 3,\sqrt{3} \right)$
We have to find the third point of the equilateral triangle. There exist 2 points which will form an equilateral triangle with A and B. Let’s assume those points are C and D.
Rotating point B with respect to A by angle $\dfrac{\pi }{3}$ anti-clock wise we will get C.
Rotating point B with respect to A by angle $\dfrac{\pi }{3}$ clock wise we will get D.
We can use complex numbers to solve that. First we have to write the coordinate in complex Cartesian form. We have write X coordinate as real part and Y coordinate as complex part of complex number, that is $\left( 0,0 \right)$ = $0+i0$ and $\left( 3,\sqrt{3} \right)$ = $3+i\sqrt{3}$ .
If we rotate anti-clockwise a point $\left( {{x}_{2}},{{y}_{2}} \right)$ with respect to the point $\left( {{x}_{1}},{{y}_{1}} \right)$ by an angle $\alpha $ we have to multiply the vector from $\left( {{x}_{1}},{{y}_{1}} \right)$ to $\left( {{x}_{2}},{{y}_{2}} \right)$ with ${{e}^{i\alpha }}$ then add the result to point$\left( {{x}_{1}},{{y}_{1}} \right)$.
Complex Cartesian form of new point after rotating.
$\left( {{x}_{1}}+i{{y}_{1}} \right)+\left[ {{x}_{2}}-{{x}_{1}}+i({{y}_{2}}-{{y}_{1}}) \right]{{e}^{i\alpha }}$
${{e}^{i\alpha }}=\cos \alpha +i\sin \alpha $
In this case, we have
$\left( 3+i\sqrt{3} \right)\times {{e}^{i\dfrac{\pi }{3}}}=\left( 3+i\sqrt{3} \right)\times \left( \dfrac{1}{2}+i\dfrac{\sqrt{3}}{2} \right)$
= $0+i2\sqrt{3}$
So, D=$\left( 0,2\sqrt{3} \right)$
By rotating $\dfrac{\pi }{3}$ clockwise we will get point D we have to multiply with ${{e}^{-i\dfrac{\pi }{3}}}$
$\left( 3+i\sqrt{3} \right)\times {{e}^{-i\dfrac{\pi }{3}}}=\left( 3+i\sqrt{3} \right)\times \left( \dfrac{1}{2}-i\dfrac{\sqrt{3}}{2} \right)$
= $3-i\sqrt{3}$
So, C=$\left( 3,-\sqrt{3} \right)$.

Note: Remember the complex Cartesian form of coordinates and how to rotate a point with respect to another fixed point. We also can use geometry to solve this question. We can find the midpoint of the given side and thus can calculate the equation of altitude through the side. The third point will lie on that altitude and at a distance of 3 units from midpoint to both directions because the ratio between lengths of side to altitude is $1:\dfrac{\sqrt{3}}{2}$.