Question

If the sum of the adjacent angles of a quadrilateral is equal to ${180^0}$, then which type of quadrilateral is it?
${\text{A}}{\text{. }}$Parallelogram
${\text{B}}{\text{. }}$Convex
${\text{C}}{\text{. }}$Concave
${\text{D}}{\text{. }}$None of the above

Answer 1

Hint: Here, we will proceed by assuming a parallelogram and using the property of the parallelogram (i.e., the interior angles of the parallelogram on the same side of the transversal are supplementary) we will obtain the given condition.

Complete step-by-step answer:

Let us consider a parallelogram PQRS as shown in the figure.

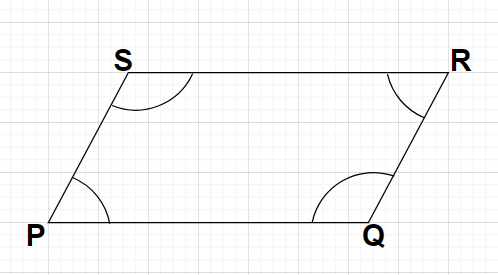
As we know that the opposite sides of a parallelogram are parallel to each other.

Here, side PQ is opposite to side RS and side QR is opposite to side SP i.e., PQ$\parallel $RS and QR$\parallel $SP.

For PQ$\parallel $RS, sides QR and SP are transversal.

According to the property of a parallelogram, the interior angles of the parallelogram on the same side of the transversal are supplementary (i.e., sum of these interior angles is ${180^0}$).

For transversal QR the two interior angles of the parallelogram PQRS on the same side are $\angle {\text{Q}}$ and $\angle {\text{R}}$.

So, $\angle {\text{Q}} + \angle {\text{R}} = {180^0}{\text{ }} \to {\text{(1)}}$

Similarly, for transversal SP the two interior angles of the parallelogram PQRS on the same side are $\angle {\text{S}}$ and $\angle {\text{P}}$.

So, $\angle {\text{S}} + \angle {\text{P}} = {180^0}{\text{ }} \to {\text{(2)}}$

For QR$\parallel $SP, sides PQ and RS are transversal.

According to the property of a parallelogram, the interior angles of the parallelogram on the same side of the transversal are supplementary (i.e., sum of these interior angles is ${180^0}$).

For transversal PQ the two interior angles of the parallelogram PQRS on the same side are $\angle {\text{P}}$ and $\angle {\text{Q}}$.

So, $\angle {\text{P}} + \angle {\text{Q}} = {180^0}{\text{ }} \to {\text{(3)}}$

Similarly, for transversal RS the two interior angles of the parallelogram PQRS on the same side are $\angle {\text{R}}$ and $\angle {\text{S}}$.

So, $\angle {\text{R}} + \angle {\text{S}} = {180^0}{\text{ }} \to {\text{(4)}}$

By combining equations (1),(2),(3) and (4), we can say that for the parallelogram PQRS the sum of adjacent angles of this quadrilateral is always equal to ${180^0}$.

Therefore, its inverse will also be true i.e., if the sum of the adjacent angles of a quadrilateral is equal to ${180^0}$, then that quadrilateral must be a parallelogram

Hence, option A is correct.

Note: In this particular problem, it is important to note that in the very beginning of the solution we have assumed the quadrilateral to be a parallelogram because the sum of the adjacent angles of any parallelogram is always equal to ${180^0}$. Also, a convex quadrilateral has an interior angle less than ${180^0}$ and a concave quadrilateral has an interior angle greater than ${180^0}$.