Question

If the segment joining the points $ (a,b) $ , $ (c,d) $ subtends a right angle at the origin, then
(A) $ ac - bd = 0 $
(B) $ ac + bd = 0 $
(C) $ ab + cd = 0 $
(D) $ ab - cd = 0 $

Answer 1

Hint: Write the coordinate on the Cartesian plane and give them some name. Form a right angle triangle by joining those points with the origin. Then find all the sides of the triangle using distance formula. And then substitute them in the Pythagoras theorem to solve the question.

Complete step-by-step answer:
Observe the diagram

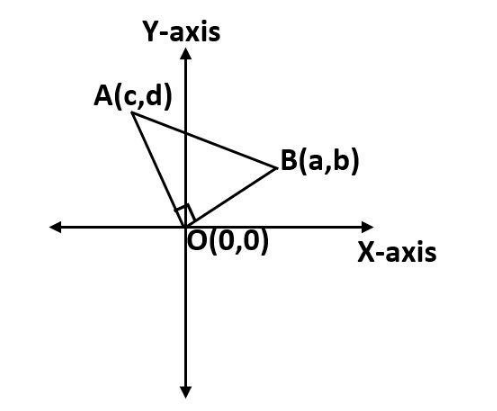
According to the question, $ (a,b),(c,d) $ subtend a right angle at the origin.
Now, observe the diagram and let us assume that A and B are the points which have the coordinates $ (c,d) $ and $ (a,b) $ respectively.
Then using distance formula, we can write
 $ O{B^2} = {a^2} + {b^2} $
 $ O{A^2} = {c^2} + {d^2} $
 $ A{B^2} = {(a - c)^2} + {(b - d)^2} $
And by using Pythagoras theorem, we can write
 $ A{B^2} = O{A^2} + O{B^2} $
By substituting the value of in the above equation, we get
 $ {(a - c)^2} + {(b - d)^2} = {c^2} + {d^2} + {a^2} + {b^2} $
Now, by using the expansion formula of square, $ {(a - b)^2} = {a^2} + {b^2} - 2ab $ , we can expand the above equation as,
 $ {a^2} + {c^2} - 2ac + {b^2} + {d^2} - 2bd = {c^2} + {d^2} + {a^2} + {b^2} $
By cancelling the common terms, we get
 $ - 2ac - 2bd = 0 $
By taking common terms out, we get
 $ - 2(ac + bd) = 0 $
 $ \Rightarrow ac + bd = 0 $
Therefore, from the above explanation, the correct answer is, option (B) $ ac + bd = 0 $
So, the correct answer is “Option B”.

Note: Always draw a rough diagram. It helps to understand what approach should be taken to solve the question. Like in this question, it became easy to observe in the diagram that we can use the Pythagoras theorem as well as distance formula and then compare the two to find the answer.