Question

If the lines \[{a_1}x + {b_1} y + {c_1} = 0\] and \[{a_2}x + {b_2} y + {c_2} = 0\] cut the coordinate axis in concyclic points, then
A ${a_1} {a_2} = {b_1} {b_2} $
B $\dfrac{{{a_1}}} {{{a_2}}} = \dfrac{{{b_1}}} {{{b_2}}} $
C ${a_1} + {a_2} = {b_1} + {b_2} $
D ${a_1} {b_1} = {a_2} {b_2} $

Answer 1

Hint: In this question we have been given equations of two lines which cut the coordinate axis in concyclic points which gives us a very important relation. Let suppose the first line intersect at the points A and B and similarly the second line at the points C and D. AB and CD are chords around the x and the y axis with origin O. Therefore, the relation between the points A, B, C, D, as they are concyclic would be $OA \times OB = OC \times OD$. We would use this relation to solve the equation further and find the relation between ${a_1}, {a_2}, {b_1}, {b_2} $.

Complete step-by-step answer:

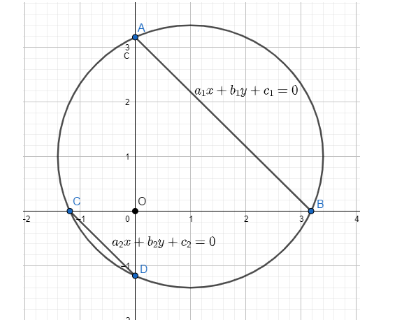
We have been provided with two equation \[{a_1}x + {b_1} y + {c_1} = 0\] and \[{a_2}x + {b_2} y + {c_2} = 0\]. So, we will be finding the coordinates of both the equations one by one.
 The first equation is \[{a_1}x + {b_1}y + {c_1} = 0\] , so the coordinates of this equation will be $A\left( {\dfrac{{ - {c_1}}}{{{a_1}}},0} \right)$ and $B\left( {0,\dfrac{{ - {c_1}}}{{{b_1}}}} \right)$
Similarly, for the second equation \[{a_2}x + {b_2}y + {c_2} = 0\], the coordinates would be $C\left( {\dfrac{{ - {c_2}}}{{{a_2}}},0} \right)$ and $D\left( {0,\dfrac{{ - {c_2}}}{{{b_2}}}} \right)$
Now these coordinate points AB and CD are chords for the x and y axis respectively around the origin O.
And since these points A, B, C, D, are concyclic the following relation would be true for them $OA \times OB = OC \times OD$.
Now keeping the values of these points in the above relation
 The values will be $\left( {\dfrac{{ - {c_1}}}{{{a_1}}}} \right) \times \dfrac{{ - {c_2}}}{{{a_2}}} = \left( {\dfrac{{ - {c_1}}}{{{b_1}}}} \right) \times \dfrac{{ - {c_2}}}{{{b_2}}}$
Now solving this equation using cross multiplication method the final relation comes out to be ${a_1} {a_2} = {b_1} {b_2} $
So, the answer comes out to be ${a_1} {a_2} = {b_1} {b_2} $ which is your option (a).
So, the correct answer is “Option A”.

Note: Whenever we are provided with options in a particular question never just try to put all the possible answers in the equation rather than try to find the hint as in this question we were provided that the coordinates are concyclic so from there we were able to obtain the relation to solve this question.