If the line \[y-\sqrt{3}x+3=0\] cuts the parabola \[{{y}^{2}}=x+2\] at \[A\] and \[B\], then
\[PA.PB\]
is equal to [where $P=\left( \sqrt{3},0 \right)$]
(a) \[\dfrac{4\left( \sqrt{3}+2 \right)}{3}\]
(b) $\dfrac{4\left( 2-\sqrt{3} \right)}{3}$
(c) \[\dfrac{4\sqrt{3}}{2}\]
(d) \[\dfrac{2\left( \sqrt{3}+2 \right)}{3}\]
Answer
Verified360.9k+ views
Hint: The parametric form of the equation of straight line, \[\dfrac{x-{{x}_{1}}}{\cos \theta }=\dfrac{y-{{y}_{1}}}{\sin \theta }=r\] is used in this question.
Complete step-by-step answer:
The line given in the question is \[y-\sqrt{3}x+3=0\] and the equation of the parabola is given as \[{{y}^{2}}=x+2\].
It is said in the question that the line cuts the parabola at points \[A\] and \[B\]. A point \[P\] with coordinates \[\left( \sqrt{3},0 \right)\] is also given. So, we can plot the graph with all the details as shown below,
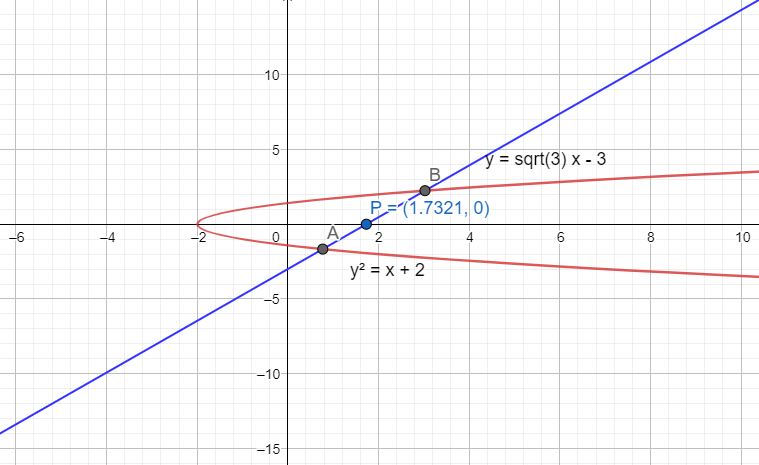
We need to find the values of \[PA\] and \[PB\] to solve the question. \[PA\] and \[PB\] represent the distance of the line joined by the points \[P,A\] and \[P,B\] respectively.
The parametric form of a straight line passing through the point $\left( {{x}_{1}},{{y}_{1}} \right)$ and making an angle of \[\theta \] with the positive direction of the x-axis is given by,
\[\dfrac{x-{{x}_{1}}}{\cos \theta }=\dfrac{y-{{y}_{1}}}{\sin \theta }=r\ldots \ldots \ldots (i)\]
where \[r\] is the distance between the two points with coordinates $\left( x,y \right)$ and $\left( {{x}_{1}},{{y}_{1}} \right)$.
In this question, \[PA\] and \[PB\] are equivalent to the distance $r$ mentioned above.
We have the coordinates of the point $\left( {{x}_{1}},{{y}_{1}} \right)=\left( \sqrt{3},0 \right)$. So, the first step is to find the angle \[\theta \].
For that, we need to consider the equation of the line and rearrange it in the slope-intercept form,
\[y-\sqrt{3}x+3=0\]
\[y=\sqrt{3}x-3\]
Comparing it with the slope-intercept form given by \[y=mx+c\], we get the slope as \[m=\sqrt{3}=\tan \theta \].
The angle \[\theta \] can hence be computed as below,
\[\begin{align}
& \tan \theta =\sqrt{3} \\
& \theta ={{\tan }^{-1}}\sqrt{3} \\
& \theta =60{}^\circ \\
\end{align}\]
Now substituting the obtained results in the equation \[(i)\],
\[\dfrac{x-\sqrt{3}}{\cos 60{}^\circ }=\dfrac{y-0}{\sin 60{}^\circ }=r\]
Substituting the values of \[\cos 60{}^\circ =\dfrac{1}{2},\sin 60{}^\circ =\dfrac{\sqrt{3}}{2}\], we get,
\[\dfrac{x-\sqrt{3}}{\dfrac{1}{2}}=\dfrac{y-0}{\dfrac{\sqrt{3}}{2}}=r\]
Equating both \[x\] and \[y\] to $r$,
\[\dfrac{x-\sqrt{3}}{\dfrac{1}{2}}=r,\dfrac{y-0}{\dfrac{\sqrt{3}}{2}}=r\]
\[\begin{align}
& x-\sqrt{3}=\dfrac{r}{2},y=\dfrac{\sqrt{3}}{2}r \\
& x=\sqrt{3}+\dfrac{r}{2},y=\dfrac{\sqrt{3}}{2}r \\
\end{align}\]
So, we have the coordinates of the point, \[A\] or \[B\] as \[\left( \sqrt{3}+\dfrac{r}{2},\dfrac{\sqrt{3}}{2}r \right)\].
As per the question, we know that this point cuts the parabola \[{{y}^{2}}=x+2\], so it can be substituted in the equation for the parabola as,
\[\begin{align}
& {{\left( \dfrac{\sqrt{3}}{2}r \right)}^{2}}=\left( \sqrt{3}+\dfrac{r}{2} \right)+2 \\
& \dfrac{3{{r}^{2}}}{4}=\dfrac{r}{2}+\left( \sqrt{3}+2 \right) \\
& \dfrac{3{{r}^{2}}}{4}-\dfrac{r}{2}-\left( \sqrt{3}+2 \right)=0 \\
\end{align}\]
This is in the form of a quadratic equation in $r$, so we can get the values of $r$ using the formula as,
\[\begin{align}
& r=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a} \\
& r=\dfrac{-\left( -\dfrac{1}{2} \right)\pm \sqrt{{{\left( -\dfrac{1}{2} \right)}^{2}}-4\times \left( \dfrac{3}{4} \right)\times -\left( \sqrt{3}+2 \right)}}{2\left( \dfrac{3}{4} \right)} \\
& r=\dfrac{\dfrac{1}{2}\pm \sqrt{\dfrac{1}{4}+\left( \dfrac{12}{4} \right)\left( \sqrt{3}+2 \right)}}{\left( \dfrac{3}{2} \right)} \\
\end{align}\]
Taking $\dfrac{1}{4}$ outside from the root,
\[\begin{align}
& r=\dfrac{\dfrac{1}{2}\pm \sqrt{\dfrac{1}{4}\left( 1+12\left( \sqrt{3}+2 \right) \right)}}{\left( \dfrac{3}{2} \right)} \\
& r=\dfrac{\dfrac{1}{2}\pm \dfrac{1}{2}\sqrt{1+12\left( \sqrt{3}+2 \right)}}{\left( \dfrac{3}{2} \right)} \\
\end{align}\]
Cancelling out $\dfrac{1}{2}$,
\[r=\dfrac{1\pm \sqrt{1+12\left( \sqrt{3}+2 \right)}}{3}\]
Therefore, we have the roots as,
\[\begin{align}
& PA=\dfrac{1+\sqrt{1+12\left( \sqrt{3}+2 \right)}}{3} \\
& PB=\dfrac{1-\sqrt{1+12\left( \sqrt{3}+2 \right)}}{3} \\
\end{align}\]
Now, we can compute \[PA.PB\] as,
\[PA.PB=\dfrac{1+\sqrt{1+12\left( \sqrt{3}+2 \right)}}{3}\times \dfrac{1-\sqrt{1+12\left( \sqrt{3}+2 \right)}}{3}\]
Applying the identity \[\left( x+y \right)\left( x-y \right)={{x}^{2}}-{{y}^{2}}\],
\[\begin{align}
& PA.PB=\dfrac{1}{9}\times \left[ {{1}^{2}}-{{\sqrt{1+12\left( \sqrt{3}+2 \right)}}^{2}} \right] \\
& PA.PB=\dfrac{1}{9}\times \left[ 1-1-12\left( \sqrt{3}+2 \right) \right] \\
& PA.PB=\dfrac{1}{9}\times \left[ -12\left( \sqrt{3}+2 \right) \right] \\
& PA.PB=\dfrac{-12}{9}\times \left( \sqrt{3}+2 \right) \\
& PA.PB=\dfrac{-4}{3}\times \left( \sqrt{3}+2 \right) \\
\end{align}\]
We have to consider the modulus for the distance, so we get the value of \[PA.PB\] as \[\left| \dfrac{-4\left( \sqrt{3}+2 \right)}{3} \right|=\dfrac{4\left( \sqrt{3}+2 \right)}{3}\].
Hence option (a) is the correct answer.
Note: The last portion of the solution can be done more easily by using the fact that the product of the roots of a quadratic equation \[a{{x}^{2}}+bx+c=0\] can be obtained as \[\dfrac{c}{a}\]. So, for this question,$\dfrac{3{{r}^{2}}}{4}-\dfrac{r}{2}-\left( \sqrt{3}+2 \right)=0$, the product of the roots \[PA\] and \[PB\] can be obtained as \[\begin{align}
& PA.PB=\dfrac{-\left( \sqrt{3}+2 \right)}{\dfrac{3}{4}} \\
& PA.PB=\dfrac{-4\left( \sqrt{3}+2 \right)}{3} \\
& PA.PB=\left| \dfrac{-4\left( \sqrt{3}+2 \right)}{3} \right|\Rightarrow \dfrac{4\left( \sqrt{3}+2 \right)}{3} \\
\end{align}\]
Complete step-by-step answer:
The line given in the question is \[y-\sqrt{3}x+3=0\] and the equation of the parabola is given as \[{{y}^{2}}=x+2\].
It is said in the question that the line cuts the parabola at points \[A\] and \[B\]. A point \[P\] with coordinates \[\left( \sqrt{3},0 \right)\] is also given. So, we can plot the graph with all the details as shown below,
We need to find the values of \[PA\] and \[PB\] to solve the question. \[PA\] and \[PB\] represent the distance of the line joined by the points \[P,A\] and \[P,B\] respectively.
The parametric form of a straight line passing through the point $\left( {{x}_{1}},{{y}_{1}} \right)$ and making an angle of \[\theta \] with the positive direction of the x-axis is given by,
\[\dfrac{x-{{x}_{1}}}{\cos \theta }=\dfrac{y-{{y}_{1}}}{\sin \theta }=r\ldots \ldots \ldots (i)\]
where \[r\] is the distance between the two points with coordinates $\left( x,y \right)$ and $\left( {{x}_{1}},{{y}_{1}} \right)$.
In this question, \[PA\] and \[PB\] are equivalent to the distance $r$ mentioned above.
We have the coordinates of the point $\left( {{x}_{1}},{{y}_{1}} \right)=\left( \sqrt{3},0 \right)$. So, the first step is to find the angle \[\theta \].
For that, we need to consider the equation of the line and rearrange it in the slope-intercept form,
\[y-\sqrt{3}x+3=0\]
\[y=\sqrt{3}x-3\]
Comparing it with the slope-intercept form given by \[y=mx+c\], we get the slope as \[m=\sqrt{3}=\tan \theta \].
The angle \[\theta \] can hence be computed as below,
\[\begin{align}
& \tan \theta =\sqrt{3} \\
& \theta ={{\tan }^{-1}}\sqrt{3} \\
& \theta =60{}^\circ \\
\end{align}\]
Now substituting the obtained results in the equation \[(i)\],
\[\dfrac{x-\sqrt{3}}{\cos 60{}^\circ }=\dfrac{y-0}{\sin 60{}^\circ }=r\]
Substituting the values of \[\cos 60{}^\circ =\dfrac{1}{2},\sin 60{}^\circ =\dfrac{\sqrt{3}}{2}\], we get,
\[\dfrac{x-\sqrt{3}}{\dfrac{1}{2}}=\dfrac{y-0}{\dfrac{\sqrt{3}}{2}}=r\]
Equating both \[x\] and \[y\] to $r$,
\[\dfrac{x-\sqrt{3}}{\dfrac{1}{2}}=r,\dfrac{y-0}{\dfrac{\sqrt{3}}{2}}=r\]
\[\begin{align}
& x-\sqrt{3}=\dfrac{r}{2},y=\dfrac{\sqrt{3}}{2}r \\
& x=\sqrt{3}+\dfrac{r}{2},y=\dfrac{\sqrt{3}}{2}r \\
\end{align}\]
So, we have the coordinates of the point, \[A\] or \[B\] as \[\left( \sqrt{3}+\dfrac{r}{2},\dfrac{\sqrt{3}}{2}r \right)\].
As per the question, we know that this point cuts the parabola \[{{y}^{2}}=x+2\], so it can be substituted in the equation for the parabola as,
\[\begin{align}
& {{\left( \dfrac{\sqrt{3}}{2}r \right)}^{2}}=\left( \sqrt{3}+\dfrac{r}{2} \right)+2 \\
& \dfrac{3{{r}^{2}}}{4}=\dfrac{r}{2}+\left( \sqrt{3}+2 \right) \\
& \dfrac{3{{r}^{2}}}{4}-\dfrac{r}{2}-\left( \sqrt{3}+2 \right)=0 \\
\end{align}\]
This is in the form of a quadratic equation in $r$, so we can get the values of $r$ using the formula as,
\[\begin{align}
& r=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a} \\
& r=\dfrac{-\left( -\dfrac{1}{2} \right)\pm \sqrt{{{\left( -\dfrac{1}{2} \right)}^{2}}-4\times \left( \dfrac{3}{4} \right)\times -\left( \sqrt{3}+2 \right)}}{2\left( \dfrac{3}{4} \right)} \\
& r=\dfrac{\dfrac{1}{2}\pm \sqrt{\dfrac{1}{4}+\left( \dfrac{12}{4} \right)\left( \sqrt{3}+2 \right)}}{\left( \dfrac{3}{2} \right)} \\
\end{align}\]
Taking $\dfrac{1}{4}$ outside from the root,
\[\begin{align}
& r=\dfrac{\dfrac{1}{2}\pm \sqrt{\dfrac{1}{4}\left( 1+12\left( \sqrt{3}+2 \right) \right)}}{\left( \dfrac{3}{2} \right)} \\
& r=\dfrac{\dfrac{1}{2}\pm \dfrac{1}{2}\sqrt{1+12\left( \sqrt{3}+2 \right)}}{\left( \dfrac{3}{2} \right)} \\
\end{align}\]
Cancelling out $\dfrac{1}{2}$,
\[r=\dfrac{1\pm \sqrt{1+12\left( \sqrt{3}+2 \right)}}{3}\]
Therefore, we have the roots as,
\[\begin{align}
& PA=\dfrac{1+\sqrt{1+12\left( \sqrt{3}+2 \right)}}{3} \\
& PB=\dfrac{1-\sqrt{1+12\left( \sqrt{3}+2 \right)}}{3} \\
\end{align}\]
Now, we can compute \[PA.PB\] as,
\[PA.PB=\dfrac{1+\sqrt{1+12\left( \sqrt{3}+2 \right)}}{3}\times \dfrac{1-\sqrt{1+12\left( \sqrt{3}+2 \right)}}{3}\]
Applying the identity \[\left( x+y \right)\left( x-y \right)={{x}^{2}}-{{y}^{2}}\],
\[\begin{align}
& PA.PB=\dfrac{1}{9}\times \left[ {{1}^{2}}-{{\sqrt{1+12\left( \sqrt{3}+2 \right)}}^{2}} \right] \\
& PA.PB=\dfrac{1}{9}\times \left[ 1-1-12\left( \sqrt{3}+2 \right) \right] \\
& PA.PB=\dfrac{1}{9}\times \left[ -12\left( \sqrt{3}+2 \right) \right] \\
& PA.PB=\dfrac{-12}{9}\times \left( \sqrt{3}+2 \right) \\
& PA.PB=\dfrac{-4}{3}\times \left( \sqrt{3}+2 \right) \\
\end{align}\]
We have to consider the modulus for the distance, so we get the value of \[PA.PB\] as \[\left| \dfrac{-4\left( \sqrt{3}+2 \right)}{3} \right|=\dfrac{4\left( \sqrt{3}+2 \right)}{3}\].
Hence option (a) is the correct answer.
Note: The last portion of the solution can be done more easily by using the fact that the product of the roots of a quadratic equation \[a{{x}^{2}}+bx+c=0\] can be obtained as \[\dfrac{c}{a}\]. So, for this question,$\dfrac{3{{r}^{2}}}{4}-\dfrac{r}{2}-\left( \sqrt{3}+2 \right)=0$, the product of the roots \[PA\] and \[PB\] can be obtained as \[\begin{align}
& PA.PB=\dfrac{-\left( \sqrt{3}+2 \right)}{\dfrac{3}{4}} \\
& PA.PB=\dfrac{-4\left( \sqrt{3}+2 \right)}{3} \\
& PA.PB=\left| \dfrac{-4\left( \sqrt{3}+2 \right)}{3} \right|\Rightarrow \dfrac{4\left( \sqrt{3}+2 \right)}{3} \\
\end{align}\]
Last updated date: 21st Sep 2023
•
Total views: 360.9k
•
Views today: 4.60k
