Question

If the area (in sq. units) of the region $\left\{ \left( x,y \right):{{y}^{2}}\le 4x,x+y\le 1,x\ge 0,y\ge 0 \right\}$ is $a\sqrt{2}+b$, then $a-b$ is equal to:
(a) $\dfrac{8}{3}$
(b) $\dfrac{10}{3}$
(c) 6
(d) $-\dfrac{2}{3}$

Answer 1

Hint: First of all draw the inequalities given in the above question and find the region which is bounded by the inequalities. After that using the method of integration, find the area bounded. We know that the area under the curve is represented by \[\int\limits_{a}^{b}{xdy}\] where a and b are the limits in which the region is bounded. Now, apply the appropriate limits in the above integral to find the area under the bounded region.

Complete step-by-step answer:
We have to find the area bounded by the following inequalities:
$\left\{ \left( x,y \right):{{y}^{2}}\le 4x,x+y\le 1,x\ge 0,y\ge 0 \right\}$
Now, in the below figure, we have drawn the above inequalities:

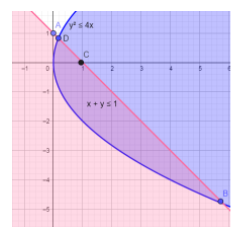
In the above diagram, as you can see that ODC (here, O is the origin) is the bounded region of which we have to find the area.
The point of intersections of the inequalities are point A, D, C so in the below, we are going to find the coordinates of these points,
Point A and point C is the intersection of line $x+y=1$ with y and x axis so finding the point A by keeping x as 0 and the point C by keeping the y coordinate as 0 we get,
Point A equal to:
$\begin{align}
  & 0+y=1 \\
 & \Rightarrow y=1 \\
\end{align}$
Hence, coordinates of point A is equal to (0, 1).
Point C is calculated by keeping y coordinate as 0 in the equation $x+y=1$ we get,
$\begin{align}
  & x+0=1 \\
 & \Rightarrow x=1 \\
\end{align}$
The coordinates of point C are equal to (1, 0).
Point D is calculated by finding the intersection of line and the parabola.
$\begin{align}
  & x+y=1 \\
 & \Rightarrow x=1-y \\
\end{align}$
${{y}^{2}}=4x$
Substituting $x=1-y$ in the above equation we get,
$\begin{align}
  & {{y}^{2}}=4\left( 1-y \right) \\
 & \Rightarrow {{y}^{2}}+4y-4=0 \\
\end{align}$
Using ShreeDharacharya formula in the above equation to find the roots of y which is given for $a{{y}^{2}}+by+c=0$ we get,
$y=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$
Now, comparing with the above equation we get the value of a, b and c as 1, 4 and -4 so substituting these values of a, b and c in the above equation we get,
$\begin{align}
  & y=\dfrac{-4\pm \sqrt{{{\left( -4 \right)}^{2}}-4\left( 1 \right)\left( -4 \right)}}{2\left( 1 \right)} \\
 & \Rightarrow y=\dfrac{-4\pm \sqrt{16+16}}{2} \\
 & \Rightarrow y=\dfrac{-4\pm 4\sqrt{2}}{2} \\
 & \Rightarrow y=-2\pm 2\sqrt{2} \\
\end{align}$
Now, we don’t need the negative value of y because the inequalities in the question above contain non negative value of x and y so the value of y is equal to:
$y=-2+2\sqrt{2}$
To find the area of the bounded region ODC, we have to subtract the region OAD from the triangle OAC we get,
Area of $\Delta AOC$ is equal to:
$\begin{align}
  & \dfrac{1}{2}\left( 1 \right)\left( 1 \right) \\
 & =\dfrac{1}{2} \\
\end{align}$
Now, we are going to find the area of region OAD as follows:
$\begin{align}
  & \int\limits_{a}^{b}{xdy} \\
 & =\int\limits_{0}^{2\sqrt{2}-2}{\dfrac{{{y}^{2}}}{4}}dy+\int\limits_{2\sqrt{2}-2}^{1}{\left( 1-y \right)}dy \\
\end{align}$
In the above integral, we are using the following integration:
$\begin{align}
  & \int{{{y}^{n}}}dy \\
 & =\dfrac{{{y}^{n+1}}}{n+1}+c \\
\end{align}$
$\begin{align}
  & \dfrac{1}{4}\left| \dfrac{{{y}^{3}}}{3} \right|_{0}^{2\sqrt{2}-2}+\left| y \right|_{2\sqrt{2}-2}^{1}-\left| \dfrac{{{y}^{2}}}{2} \right|_{2\sqrt{2}-2}^{1} \\
 & =\dfrac{1}{12}\left[ {{\left( 2\sqrt{2}-2 \right)}^{3}}-0 \right]+1-\left( 2\sqrt{2}-2 \right)-\dfrac{1}{2}\left[ {{\left( 1 \right)}^{2}}-{{\left( 2\sqrt{2}-2 \right)}^{2}} \right] \\
\end{align}$
$\begin{align}
  & =\dfrac{1}{12}{{\left( 2 \right)}^{3}}{{\left( \sqrt{2}-1 \right)}^{3}}+3-2\sqrt{2}-\dfrac{1}{2}\left[ 1-\left( 8+4-8\sqrt{2} \right) \right] \\
 & =\dfrac{8}{12}\left[ {{\left( \sqrt{2} \right)}^{3}}-3{{\left( \sqrt{2} \right)}^{2}}+3\left( \sqrt{2} \right)-1 \right]+3-2\sqrt{2}-\dfrac{1}{2}\left[ 8\sqrt{2}-11 \right] \\
 & =\dfrac{2}{3}\left[ 2\sqrt{2}-3\left( 2 \right)+3\left( \sqrt{2} \right)-1 \right]+3-2\sqrt{2}-4\sqrt{2}+\dfrac{11}{2} \\
 & =\dfrac{23}{6}-\dfrac{8}{3}\sqrt{2} \\
\end{align}$
Now, we have to subtract the above area from the area of triangle OAC to get the area of the bounded region.
$\begin{align}
  & \dfrac{1}{2}-\left( \dfrac{23}{6}-\dfrac{8}{3}\sqrt{2} \right) \\
 & =\dfrac{1}{2}-\dfrac{23}{6}+\dfrac{8}{3}\sqrt{2} \\
 & =\dfrac{3-23}{6}+\dfrac{8}{3}\sqrt{2} \\
 & =-\dfrac{20}{6}+\dfrac{8}{3}\sqrt{2} \\
\end{align}$
Now, it is given that the area bounded by the inequalities is equal to $a\sqrt{2}+b$ so equating the above area to $a\sqrt{2}+b$ we get,
$-\dfrac{20}{6}+\dfrac{8}{3}\sqrt{2}=a\sqrt{2}+b$
From the above, we get the values of a and b as:
$a=\dfrac{8}{3},b=-\dfrac{20}{6}$
And the value of $a-b$ is equal to:
$\begin{align}
  & a-b=\dfrac{8}{3}+\dfrac{20}{6} \\
 & \Rightarrow a-b=\dfrac{\left( 16+20 \right)}{6} \\
 & \Rightarrow a-b=\dfrac{36}{6} \\
 & \Rightarrow a-b=6 \\
\end{align}$
Hence, the correct option is (c).

Note: The place where you make the mistake is by not subtracting the area of triangle OAC in the area of region OAD because the calculation for the area of region OAD is very tedious and after solving that we got excited and forget to subtract the area of triangle OAC. The other reason due to which you forgot to subtract the area of triangle OAC is that the result of the area of region OAD is in the form of $a\sqrt{2}+b$ which is given in the question so you think that yeah, this is the correct answer so make sure you won’t commit that mistake in the exam.