Question

If given a trigonometric equation$\sqrt 3 \tan \theta = 3\sin \theta $, find the value of ${\sin ^2}\theta - {\cos ^2}\theta $

Answer 1

Hint: - Use the trigonometric identities and Pythagoras theorem.

Given:$\sqrt 3 \tan \theta = 3\sin \theta $
$
   \Rightarrow \tan \theta = \dfrac{3}{{\sqrt 3 }}\sin \theta \\
   \Rightarrow \tan \theta = \sqrt 3 \sin \theta \\
   \Rightarrow \dfrac{{\tan \theta }}{{\sin \theta }} = \sqrt 3 \\
   \Rightarrow \cos \theta = \dfrac{1}{{\sqrt 3 }} \\
   \Rightarrow \cos \theta = \dfrac{{Adjacent{\text{ }}side}}{{Hypotenuse}} = \dfrac{B}{H} = \dfrac{1}{{\sqrt 3 }} \\
 $

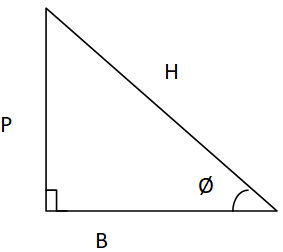
From the above figure for the Right angled triangle by using Pythagoras Theorem,
$
  {H^2} = {P^2} + {B^2} \\
  {\left( {\sqrt 3 } \right)^2} = {P^2} + {1^2} \\
  {P^2} = 3 - 1 \\
  {P^2} = 2 \\
  P = \sqrt 2 \\
$
Now, ${\sin ^2}\theta - {\cos ^2}\theta = {\left( {\dfrac{P}{H}} \right)^2} - {\left( {\dfrac{B}{H}} \right)^2}$
$
   = {\left( {\dfrac{{\sqrt 2 }}{{\sqrt 3 }}} \right)^2} - {\left( {\dfrac{1}{{\sqrt 3 }}} \right)^2} \\
   = \dfrac{2}{3} - \dfrac{1}{3} \\
   = \dfrac{1}{3} \\
$
Note: The above question can be solved by using trigonometric identities, but here it is done by visualizing the terms in the form of sides of the right angled triangle, thus making the problem easier to solve.