Question

If $E_{_{A{u^ + }/Au}}^0 = 1.69V$and $E_{A{u^{ + 3}}/Au}^0 = 1.40V$then $E_{A{u^ + }/A{u^{3 + }}}^0$ will it be?
A.$0.19V$
B.$2.495V$
C.$ - 2.5V$
D.$ - 1.255V$

Answer 1

Hint:The electrode potential is the electromotive force of a galvanic cell which is calculated as the standard reference electrode and another electrode. We take the electrode potential of anode on the left and electrode potential of cathode on the right. This gives us the electromotive force of a cell.
Formula used:
${n_3}{E_3} = {n_2}{E_2} + {n_1}{E_1}$

Complete step by step answer:
The potential difference between the two electrodes of a galvanic cell is known as the cell potential which is calculated in volts and the cell potential is calculated as the difference between the electrode potentials of the cathode and anode. We take the electrode potential of anode on the left and electrode potential of cathode on the right. This gives us the electromotive force of a cell. Thus, electrode potential is the electromotive force of a galvanic cell which is calculated as the standard reference electrode and another electrode.
${E_{cell}} = {E_{cathode}} + {E_{anode}}$
The hydrogen electrode is taken as the standard electrode as it is meant to have a potential of zero volts. Oxidation occurs at the anode and reduction occurs at the cathode.
${H^ + }(aq) + {e^ - } = \dfrac{1}{2}{H_2}(g)$
For the above question, it is given that
$E_{_{A{u^ + }/Au}}^0 = 1.69V$
$ \Rightarrow A{u^ + } + 1{e^ - } \to Au$
$E_{A{u^{ + 3}}/Au}^0 = 1.40V$
$ \Rightarrow A{u^{3 + }} + 3{e^ - } \to Au$
${E_{A{u^ + }/A{u^{ + 3}}}} \Rightarrow A{u^ + } \to A{u^{ + 3}} + 2{e^ - }$

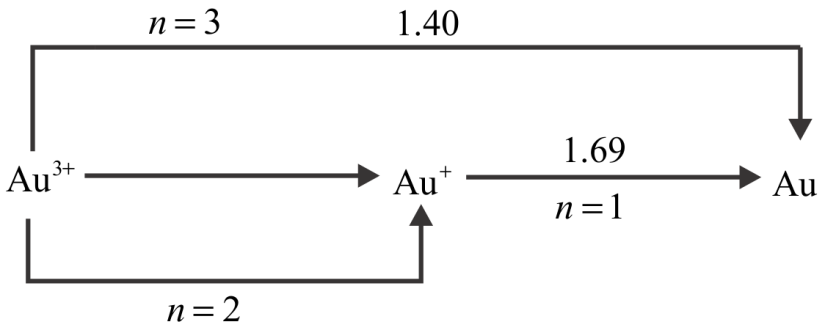
We know that,
${n_3}{E_3} = {n_2}{E_2} + {n_1}{E_1}$
$ \Rightarrow 3 \times 1.40 = 1 \times 1.69 + 2 \times E_{A{u^{3 + }}/A{u^ + }}^0$
${E^0}_{A{u^{3 + }}/A{u^ + }} = \dfrac{{4.20 - 1.69}}{2}$
$ \Rightarrow {E^0}_{A{u^{3 + }}/A{u^ + }} = 1.255$
We have to calculate $E_{A{u^ + }/A{u^{3 + }}}^0$
$ \Rightarrow E_{A{u^ + }/A{u^{3 + }}}^0 = - E_{A{u^{3 + }}/A{u^ + }}^0$
$ \Rightarrow E_{A{u^ + }/A{u^{3 + }}}^0 = - 1.255$

Hence, the correct option is (D) .

The reduced form of an electrode is more stable than the hydrogen electrode if its standard electrode potential is greater than zero.

Note:
Platinum and gold are metals which are used as electrodes and are known as inert electrodes because they do not react in the reaction and instead provide their surface for reactions like oxidation and reduction to take place and conduct electrons and complete the galvanic cell circuit.