Question

If direction cosines of two lines are proportional to \[(2,3. - 6)\] and \[(3, - 4,5)\]then the acute angle between them is
A.${\cos ^{ - 1}}(\dfrac{{49}}{{36}})$
B.${\cos ^{ - 1}}(\dfrac{{18\sqrt 2 }}{{35}})$
C.${96^ \circ }$
D.${\cos ^{ - 1}}(\dfrac{{18}}{{35}})$

Answer 1

Hint: In the given question, we have to find the angle between two lines, say a and b as shown in diagram.

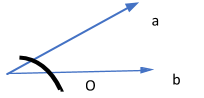
The dot product of a and b is given by
$ \Rightarrow \overrightarrow a .\overrightarrow b = |\overrightarrow a ||\overrightarrow b |\cos \phi $
$ \Rightarrow \phi = {\cos ^{ - 1}}(\dfrac{{\overrightarrow a .\overrightarrow b }}{{|\overrightarrow a ||\overrightarrow b |}})$ ………………….(1)

Complete step-by-step answer:
First of all, find the value of $\overrightarrow a \& \overrightarrow b $i.e.
$
   \Rightarrow \overrightarrow a = \overrightarrow {OA} = 2\mathop i\limits^ \wedge + 3\mathop j\limits^ \wedge - 6\mathop k\limits^ \wedge \\
   \Rightarrow \overrightarrow b = \overrightarrow {OB} = 3\mathop i\limits^ \wedge - 4\mathop j\limits^ \wedge + 5\mathop k\limits^ \wedge \\
$
After that find the value of $|\overrightarrow a ||\overrightarrow b |$, for we have to find $|\overrightarrow a |\& |\overrightarrow b |$as follows:
$
   \Rightarrow |\overrightarrow a | = \sqrt {{a_1}^2 + {b_1}^2 + {c_1}^2} \\
   \Rightarrow |\overrightarrow a | = \sqrt {{2^2} + {3^2} + {{( - 6)}^2}} \\
   \Rightarrow |\overrightarrow a | = \sqrt {4 + 9 + 36} \\
   \Rightarrow |\overrightarrow a | = \sqrt {49} = 7 \\
$
$
   \Rightarrow |\overrightarrow a | = \sqrt {{x_2}^2 + {y_2}^2 + {z_3}^2} \\
   \Rightarrow |\overrightarrow a | = \sqrt {{3^2} + {{( - 4)}^2} + {5^2}} \\
   \Rightarrow |\overrightarrow a | = \sqrt {9 + 16 + 25} \\
   \Rightarrow |\overrightarrow a | = \sqrt {50} = 5\sqrt 2 \\
$
$ \Rightarrow |\overrightarrow a | = 5\sqrt 2 $ …………………….(2)
Therefore, value of $|\overrightarrow a ||\overrightarrow b |$ is
$ \Rightarrow |\overrightarrow a ||\overrightarrow b | = 7 \times 5\sqrt 2 = 35\sqrt 2 $
Now, find the value of $\overrightarrow a .\overrightarrow b $ as given below
$
   \Rightarrow \overrightarrow a .\overrightarrow b = ({x_1}\mathop i\limits^ \wedge + {y_1}\mathop j\limits^ \wedge + {z_1}\mathop {k)}\limits^ \wedge ({x_2}\mathop i\limits^ \wedge + {y_2}\mathop j\limits^ \wedge + {z_2}\mathop {k)}\limits^ \wedge \\
   \Rightarrow \overrightarrow a .\overrightarrow b = (2\mathop i\limits^ \wedge + 3\mathop j\limits^ \wedge + ( - 6)\mathop {k)}\limits^ \wedge (3\mathop i\limits^ \wedge + ( - 4)\mathop j\limits^ \wedge + 5\mathop {k)}\limits^ \wedge \\
   \Rightarrow \overrightarrow a .\overrightarrow b = (2 \times 3) + (3 \times ( - 4)) + (( - 6) \times 5) \\
   \Rightarrow \overrightarrow a .\overrightarrow b = 6 - 12 - 30 = - 36 \\
$
$ \Rightarrow \overrightarrow a .\overrightarrow b = - 36$ ……………………..(3)
For finding $\phi $ put the values of 2 and 3 in equation 1, we get
$ \Rightarrow \phi = {\cos ^{ - 1}}(\dfrac{{\overrightarrow a .\overrightarrow b }}{{|\overrightarrow a ||\overrightarrow b |}})$
$
   \Rightarrow \phi = {\cos ^{ - 1}}(\dfrac{{ - 36}}{{35\sqrt 2 }}) \\
   \Rightarrow \phi = {\cos ^{ - 1}}(\dfrac{{36}}{{35\sqrt 2 }}) \\
   \Rightarrow \phi = {\cos ^{ - 1}}(\dfrac{{36\sqrt 2 }}{{35\sqrt 2 \sqrt 2 }}) = {\cos ^{ - 1}}(\dfrac{{36\sqrt 2 }}{{35 \times 2}}) \\
   \Rightarrow \phi = {\cos ^{ - 1}}(\dfrac{{18\sqrt 2 }}{{35}}) \\
$
The required answer is $\phi = {\cos ^{ - 1}}(\dfrac{{18\sqrt 2 }}{{35}})$
 So, the correct option is B.

Note: Some students get confused and don't take O points and form the angle. So, to do these types of questions assume a point where angle is formed.
For cosine direction take scalar product and for sine direction take cross product.
Also, students take negative values as they forget to apply the concept of trigonometry i.e. $\cos \theta = \cos ( - \theta )$. What in this question negative value is given in options but if in options negative value is given, don’t mark that option. Your answer can get wrong, take care of this.