
If $\dfrac{{x - 1}}{{x + 1}} = \dfrac{7}{9}$ then $x = ?$
a. $6$
b. $7$
c. $8$
d. $10$
Answer
534.6k+ views
Hint:We have to solve the mathematical expression by cross multiplication method. For that we need to multiply the denominator of the right-hand side to the numerator of the left-hand side and opposite to the other side. And then will form a linear equation, and the value of x is found.
Complete step by step solution:
In the above question, we are given an expression
$\dfrac{{x - 1}}{{x + 1}} = \dfrac{7}{9}$ and we had to find the value for x.
So, doing cross multiplication
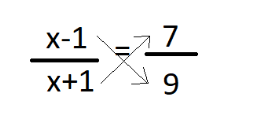
$9\left( {x - 1} \right) = 7\left( {x + 1} \right)$
Hence, multiplying into the brackets
$9x - 9x = 7x + 7$
Taking the variables to the left-hand side and constants to the right-hand side.
$9x - 7x = 7 + 9$
So, $2x = 16$
Finding the value of x by dividing both sides by $2$
$ \Rightarrow x = \dfrac{{16}}{2} = 8$
Hence, the value of x is $8$
Note: While taking the variables to the left-hand side or right-hand side sign will always change but not in the case for division. In the first step we are just going cross multiplication. But be careful while adding or subtracting where signs will change on changing the sides.
Complete step by step solution:
In the above question, we are given an expression
$\dfrac{{x - 1}}{{x + 1}} = \dfrac{7}{9}$ and we had to find the value for x.
So, doing cross multiplication
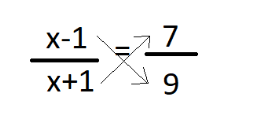
$9\left( {x - 1} \right) = 7\left( {x + 1} \right)$
Hence, multiplying into the brackets
$9x - 9x = 7x + 7$
Taking the variables to the left-hand side and constants to the right-hand side.
$9x - 7x = 7 + 9$
So, $2x = 16$
Finding the value of x by dividing both sides by $2$
$ \Rightarrow x = \dfrac{{16}}{2} = 8$
Hence, the value of x is $8$
Note: While taking the variables to the left-hand side or right-hand side sign will always change but not in the case for division. In the first step we are just going cross multiplication. But be careful while adding or subtracting where signs will change on changing the sides.
Recently Updated Pages
Master Class 11 Chemistry: Engaging Questions & Answers for Success

Which is the Longest Railway Platform in the world?

India Manned Space Mission Launch Target Month and Year 2025 Update

Which of the following pairs is correct?

The Turko-Afghan rule in India lasted for about?

Who wrote the novel "Pride and Prejudice"?

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

Which type of resource is iron ore A Renewable B Biotic class 11 social science CBSE

10 examples of friction in our daily life

Differentiate between an exothermic and an endothermic class 11 chemistry CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




