Question

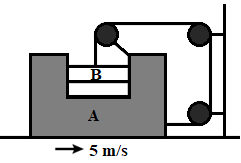
If block A is moving with an acceleration of $5m{{s}^{-2}}$, the acceleration of B with respect to ground is.

$\begin{align}
  & \text{A}\text{. }5m{{s}^{-2}} \\
 & \text{B}\text{. }5\sqrt{2}m{{s}^{-2}} \\
 & \text{C}\text{. }5\sqrt{5}m{{s}^{-2}} \\
 & \text{D}\text{. }10m{{s}^{-2}} \\
\end{align}$

Answer 1

Hint: The force and the action of a pulley system can be calculated using the newton’s law of motion. We will first name the different length of thread and apply length constraint theorem. The total length of thread will remain the same. From the equation between different lengths of threads, we will double differentiate to get a relation between acceleration of different lengths of thread. We will find the resultant acceleration using vector addition and use the given acceleration of A to find the acceleration of B.

Complete step by step answer:
A pulley can be described as a mounted rotating wheel having a curved convex rim with a rope, a chain or a belt that can move along the wheel's rim to change the direction of a pulling force. Pulley is used to modify or reduce the amount of effort needed to move heavy objects such as automobile engines and elevators.
We can calculate the force and action of a pulley system through the application of Newton's laws of motion. The second law deals with the force and the acceleration, while the third law indicates the direction of the forces and how the force of tension balances the gravitational force.
We are given a pulley system having a block A which moves with an acceleration of $5m{{s}^{-2}}$ and we need to calculate the acceleration of B.
We will use the law of constraints to solve this problem, according to which the total length of thread will remain the same. Thread released from one end will accumulate on the other end.

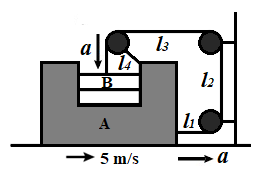
When block A is our reference,
Length of string is,
$l={{l}_{1}}+{{l}_{2}}+{{l}_{3}}+{{l}_{4}}$
By double differentiating both sides with respect to time,
$\dfrac{{{d}^{2}}}{d{{t}^{2}}}\left( l \right)=\dfrac{{{d}^{2}}}{d{{t}^{2}}}\left( {{l}_{1}} \right)+\dfrac{{{d}^{2}}}{d{{t}^{2}}}\left( {{l}_{2}} \right)+\dfrac{{{d}^{2}}}{d{{t}^{2}}}\left( {{l}_{3}} \right)+\dfrac{{{d}^{2}}}{d{{t}^{2}}}\left( {{l}_{4}} \right)$
As, total length of thread is a constraint
So,
$\dfrac{{{d}^{2}}}{d{{t}^{2}}}\left( l \right)=0$
Or,
$0={{a}_{1}}+{{a}_{2}}+{{a}_{3}}+{{a}_{4}}$
Decrease in length of ${{l}_{1}}$ and ${{l}_{3}}$ will be same,
So,
${{a}_{1}}={{a}_{3}}=a$
Also, distance between the two pulleys fixed on the walls is fixed, so
${{a}_{2}}=0$
Therefore,
$\begin{align}
  & 0=a+0+a+{{a}_{4}} \\
 & -2a={{a}_{4}} \\
\end{align}$
Now,
With respect to ground, acceleration of block B is given as,
$\overrightarrow{{{a}_{B}}}=\overrightarrow{{{a}_{4}}}+\overrightarrow{a}$
Where, both vectors are perpendicular to each other.
Magnitude of acceleration of B with respect to ground,
$\begin{align}
  & \left| \overrightarrow{{{a}_{B}}} \right|=\left| \overrightarrow{{{a}_{4}}}+\overrightarrow{a} \right| \\
 & {{a}_{B}}=\left| \overrightarrow{{{a}_{4}}}+\overrightarrow{a} \right| \\
 & {{a}_{B}}=\sqrt{{{\left( {{a}_{4}} \right)}^{2}}+{{\left( a \right)}^{2}}+2\times \left( {{a}_{4}} \right)\times \left( a \right)} \\
\end{align}$
Put,
${{a}_{4}}=-2a$
$\begin{align}
  & {{a}_{B}}=\sqrt{{{\left( -2a \right)}^{2}}+{{\left( a \right)}^{2}}+2\times \left( -2a \right)\times \left( a \right)} \\
 & {{a}_{B}}=\sqrt{4{{a}^{2}}+{{a}^{2}}+0} \\
 & {{a}_{B}}=\sqrt{5{{a}^{2}}} \\
 & {{a}_{B}}=\sqrt{5}a \\
\end{align}$
We have,
$a=5m{{s}^{-2}}$
Therefore,
${{a}_{B}}=5\sqrt{5}m{{s}^{-2}}$
The acceleration of B with respect to ground is $5\sqrt{5}m{{s}^{-2}}$

So, the correct answer is “Option C”.

Note:
Length constraint theorem can be applied in pulley problems, where we can assume the length of free thread will remain constant. This theorem can be used to obtain both velocity and acceleration of different pulleys or objects attached to them in a complicated pulley system.
Single derivative of the constraint equation gives the result of relation between velocities and double derivative gives relation between acceleration of different lengths of thread, or objects attached to them.