Question

If area between $y=m{{x}^{2}},x=m{{y}^{2}}$ (m > 0) is $\dfrac{1}{4}$ sq . units, then value of m is
A. $\pm 3\sqrt{2}$
B. $\pm \dfrac{2}{\sqrt{3}}$
C. $\sqrt{2}$
D. $\sqrt{3}$

Answer 1

Hint: Find the intersection of both the parabolas given in problem. Draw a neat diagram to get an accurate bounded area. A area of any curve f(x) with x-axis from x = a to x = b is given as
$Area=\int_{a}^{b}{f\left( x \right)}dx$
Equate the given area to the calculated area.

Complete answer:
Find the intersection of both the parabolas given in problem. Draw a neat diagram to get an accurate bounded area. A area of any curve f(x) with x-axis from x = a to x = b is given as
$Area=\int_{a}^{b}{f\left( x \right)}dx$
Equate the given area to the calculated area.
Here, it is given that area between the curves $y=m{{x}^{2}},x=m{{y}^{2}}$ (m > 0) is $\dfrac{1}{4}$ sq . units, then we need to determine the value of ‘m’.
As, both the curves are representing parabola of the forms of ${{y}^{2}}=4ax,{{x}^{2}}=4ay\to y=m{{x}^{2}}$can be written as ${{x}^{2}}=\dfrac{1}{m}y,x=m{{y}^{2}}$ can be written as ${{y}^{2}}=\dfrac{1}{m}x$
Hence, we can represent the given equations in form of parabolas ${{x}^{2}}=\dfrac{1}{m}y,{{y}^{2}}=\dfrac{1}{m}x$ as

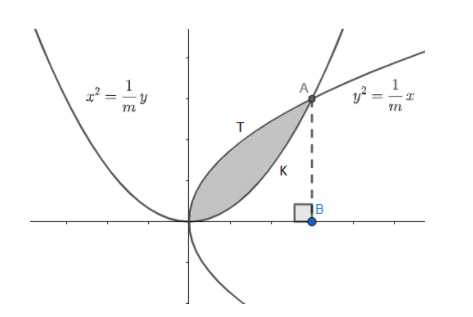
So, the area bounded by both the parabolas given in the question are represented by the shaded region in the above diagram. Hence, we need to calculate the area of OAO.
So, area of shaded region can be calculated by the difference of the area by ${{y}^{2}}=\dfrac{1}{m}x$ with x-axis in first quadrant and the area by ${{x}^{2}}=\dfrac{1}{m}y$ with the x-axis in first quadrant only.
Hence, we can get area of shaded region as
Area of shaded region = (area of OTAB – area of OKAB)
So, area OTAB and OKAB can be calculated with help of integration.
So, let us find the intersection point of both the parabolas i.e. A.
So, we have
${{y}^{2}}=\dfrac{1}{m}x$ ………………. (i)
${{x}^{2}}=\dfrac{1}{m}y$ ……………… (ii)
Put the value of x from equation (i) i.e. $x=m{{y}^{2}}$to the equation (ii). So, we get
$\begin{align}
  & {{\left( m{{y}^{2}} \right)}^{2}}=\dfrac{y}{m} \\
 & {{m}^{2}}{{y}^{4}}=\dfrac{y}{m} \\
 & {{m}^{3}}{{y}^{4}}-y=0 \\
 & y\left[ {{m}^{3}}{{y}^{3}}-1 \right]=0 \\
\end{align}$
y = 0, ${{m}^{3}}{{y}^{3}}-1=0$
y = 0,${{m}^{3}}{{y}^{3}}-1=0$
y = 0,${{y}^{3}}=\dfrac{1}{{{m}^{3}}}$
y = 0,$y=\dfrac{1}{m}$
So, put y = 0 to any equation (i) or (ii), we get x = 0.
Now, put $y=\dfrac{1}{m}$ to equation (i) to get the value of x. So, we get
$\begin{align}
  & {{\left( \dfrac{1}{m} \right)}^{2}}=\dfrac{1}{m}x \\
 & x=\dfrac{1}{m} \\
\end{align}$
Hence, point A is given as $\left( \dfrac{1}{m},\dfrac{1}{m} \right)$ because x = 0, y = 0 i.e. (0, 0) represents origin, so, we cannot take (0, 0) as point A.
Hence, we can get area of OTAK as
Area of shaded region = area of OTAB – area of OKAB.
So, we can get area of OTAB by integrating
${{y}^{2}}=\dfrac{1}{m}x\to y=\sqrt{\dfrac{x}{m}}$ from $0\to \dfrac{1}{m}$ as AB can be represented as $x=\dfrac{1}{m}$, Similarly area of OKAB can be calculated by integrating ${{x}^{2}}=\dfrac{1}{m}y\to y=m{{x}^{2}}$ from $o\to \dfrac{1}{m}$ .
So, we get
Area of shaded region
$\begin{align}
  & =\int\limits_{0}^{\left( \dfrac{1}{m} \right)}{\dfrac{\sqrt{x}}{\sqrt{m}}}dx-\int\limits_{0}^{\left( \dfrac{1}{m} \right)}{m{{x}^{2}}dx}, \\
 & =\dfrac{1}{\sqrt{m}}\int\limits_{0}^{\left( \dfrac{1}{m} \right)}{\sqrt{x}}dx-m\int\limits_{0}^{\left( \dfrac{1}{m} \right)}{{{x}^{2}}}dx \\
\end{align}$
We know $\int{{{x}^{n}}}dx=\dfrac{{{x}^{n+1}}}{n+1}$
So, we get
Area of shaded region =
$\begin{align}
  & \dfrac{1}{\sqrt{m}}{{\left[ \dfrac{{{x}^{\dfrac{1}{2}+1}}}{\dfrac{1}{2}+1} \right]}_{0}}^{\left( \dfrac{1}{m} \right)}-m{{\left[ \dfrac{{{x}^{3}}}{3} \right]}_{0}}^{^{\left( \dfrac{1}{m} \right)}}, \\
 & =\dfrac{1}{\sqrt{m}}\dfrac{2}{3}{{\left[ {{x}^{\dfrac{3}{2}}} \right]}_{0}}^{\left( \dfrac{1}{m} \right)}-\dfrac{m}{3}{{\left[ {{x}^{3}} \right]}_{0}}^{\left( \dfrac{1}{m} \right)}, \\
 & =\dfrac{1}{\sqrt{m}}\dfrac{2}{3}\left( {{\left( \dfrac{1}{m} \right)}^{\dfrac{3}{2}}}-0 \right)-\dfrac{m}{3}\left( {{\left( \dfrac{1}{m} \right)}^{3}}-0 \right), \\
 & =\dfrac{2}{3\sqrt{m}}\times \dfrac{1}{{{m}^{\dfrac{3}{2}}}}-\dfrac{m}{3{{m}^{3}}}, \\
 & =\dfrac{2}{3{{m}^{\dfrac{1}{2}+\dfrac{3}{2}}}}-\dfrac{1}{3{{m}^{2}}} \\
 & =\dfrac{2}{3{{m}^{2}}}-\dfrac{1}{3{{m}^{2}}}=\dfrac{1}{3{{m}^{2}}} \\
\end{align}$
Hence,
Area of the shaded region = $\dfrac{1}{3{{m}^{2}}}$
As, it is given that the area bounded by the given parabolas id $\dfrac{1}{4}$.
So, we get
$\begin{align}
  & \dfrac{1}{3{{m}^{2}}}=\dfrac{1}{4},3{{m}^{2}}=4 \\
 & {{m}^{2}}=\dfrac{4}{3} \\
 & m=\pm \dfrac{2}{\sqrt{3}} \\
\end{align}$
Hence, option (b) is the correct answer.

Note: Another approach for the area of bounded region would be that we can calculate it w.r.t. ‘dy’ (y-axis) as well. Here, we need to integrate $x=m{{y}^{2}},x=\dfrac{y}{\sqrt{m}}$ from $0\to '\dfrac{1}{m}'$ with respect to ‘dy’ and hence find the difference of them to get the required area.
One may get confused with the equation ${{m}^{3}}{{y}^{3}}=1,{{m}^{3}}{{y}^{3}}-1=0$. As, we calculated the value of $y\to \dfrac{1}{m}$ only, but one may think that there are other two values of y that are possible as well. But, we know the one root of ${{x}^{3}}=1\to 1$. And other roots of equation ${{x}^{3}}=1\to w,{{w}^{2}}$ which are non-real numbers, hence, we can relate this equation with ${{m}^{3}}{{y}^{3}}=1,{{y}^{3}}=\dfrac{1}{{{m}^{3}}}$. So, another two roots of the equation will be imaginary, except the root $\dfrac{1}{m}$. And one may observe that the intersection of both the parabolas is one point. So, other values of ‘y’ except $'\dfrac{1}{m}'$ will not be real.