Question

If \[\angle RPQ={{45}^{\circ }}\], find \[\angle PRQ\]
A. \[{{60}^{\circ }}\]
B. \[{{90}^{\circ }}\]
C. \[{{120}^{\circ }}\]
D. \[{{150}^{\circ }}\]

Answer 1

Hint: Consider, \[\vartriangle PQR\], use the properties of the isosceles triangle and find the \[\angle PRQ\]. PR and QR are tangents from a point R meeting the circle at P and Q.

“Complete step-by-step answer:”
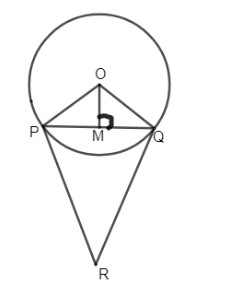
Given a figure, with a circle whose center is O. From the figure we can say that PR and QR are tangents to the circle from a point R. Three tangents from an external point to the circle are equal.
\[\therefore PR=QR\]
Now let us consider the isosceles triangle, \[\vartriangle PRQ\].
As it is an isosceles triangle, we know that two sides of an isosceles triangle are equal.
In \[\vartriangle PRQ\], we know that PR = QR.
Thus the angle RPQ is equal to angle PQR, because they are the base angles of an isosceles triangle.
We have been given, \[\angle RPQ={{45}^{\circ }}\].
\[\angle RPQ=\angle PQR={{45}^{\circ }}\].
The angle sum property of triangle, states that the sum of interior angles of a triangle is \[{{180}^{\circ }}\].
Hence, in the isosceles triangle PRQ, the sum of all the interior angles is \[{{180}^{\circ }}\].
\[\therefore \angle RPQ+\angle PQR+\angle PRQ={{180}^{\circ }}\]
We need to find the \[\angle PRQ\].
We already found out that, \[\angle RPQ=\angle PQR={{45}^{\circ }}\].
Thus substituting these values in the sum of triangle,
\[\begin{align}
  & \angle RPQ+\angle PQR+\angle PRQ={{180}^{\circ }} \\
 & {{45}^{\circ }}+{{45}^{\circ }}+\angle PRQ={{180}^{\circ }} \\
 & \angle PRQ=180-45-45=180-90 \\
 & \angle PRQ={{90}^{\circ }} \\
\end{align}\]
Hence, we got \[\angle PRQ={{90}^{\circ }}\], which makes \[\vartriangle PRQ\] right angled at R.
\[\therefore \]Option (b) is the correct answer.

Note: By seeing the figure, you may try to take \[\vartriangle POQ\] instead of \[\vartriangle PRQ\], understand the question that we only need to find \[\angle PRQ\]. So we should take, \[\vartriangle PRQ\]. As tangents from the external point of the circle are equal, the sides of the triangle are same, thus angles are same and we can get \[\angle PRQ\]easily.