Question

How do you graph $y=3-\cos x$?

Answer 1

Hint: For graphing the function which is given in the question as $y=3-\cos x$, we first have to draw the graph of the function $y=\cos x$. Then, we have to obtain the graph of the $y=-\cos x$ from the graph of $y=\cos x$ by taking the reflection of the graph of $y=\cos x$ with respect to the x axis. Finally, the graph of the function $y=3-\cos x$ will be obtained from the graph of the function $y=3-\cos x$ by shifting its graph by three units in the vertical direction.

Complete step by step answer:
From the equation given in the question, we have
$y=3-\cos x......(i)$
We can see that it is related to the basic cosine function, which is given by
$y=\cos x.......(ii)$
The graph corresponding to the above equation is, as we know drawn as

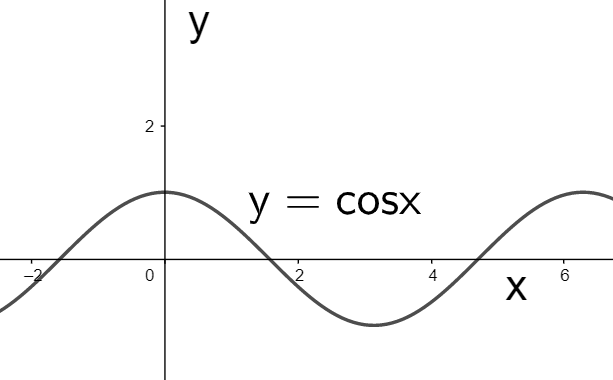
But as we can see in equation (i) that it has negative of $\cos x$. So we have to obtain the graph of
\[\Rightarrow y=-\cos x.......(ii)\]
By comparing equations (ii) and (iii) we can see that the only change is the negative of the dependent variable $y$. So its graph will be obtained by taking the reflection of the above graph with respect to the x-axis, as shown below

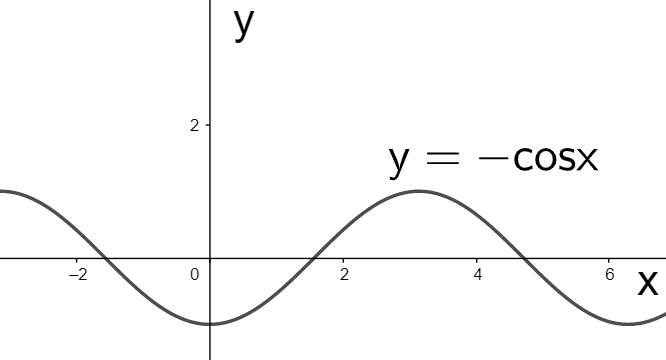
Considering the given equation
\[\begin{align}
  & \Rightarrow y=3-\cos x \\
 & \Rightarrow \left( y-3 \right)=-\cos x.......(iii) \\
\end{align}\]
By comparing (ii) and (iii) we see that the only change is that $3$ in subtracted from the dependent variable $y$. So we need to shift the above graph by $3$ units vertically to obtain the final graph as

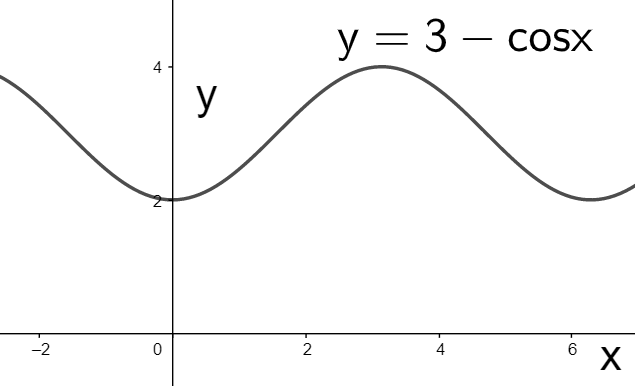
Hence, we have drawn the graph of $y=3-\cos x$

Note: Do not do the shifting of the graph before inverting it. Always remember that the shifting of the dependent variable is always done after scaling or inverting it. Also, we must not be confused regarding the direction of shifting. We might argue that as the sign of $3$ in $\left( y-3 \right)$ is negative, the graph must be shifted in the downward direction. But it must be remembered as a key point that the shifting is always done in the opposite direction.