Question

How do you graph \[r=4\sin \theta \] ?

Answer 1

Hint: These types of problems are pretty straight forward and are very easy to solve. For solving such problems we first need to understand the meaning of all the parameters used in the given problem equation. In the given sum, let us assume \[\left( x,y \right)\] as a point in the coordinate plane. The distance of this point from the origin is represented by \[r\] and is defined by \[r=\sqrt{{{x}^{2}}+{{y}^{2}}}\]. The angle that the line joining the point and the origin makes with the x-axis is represented by \[\theta \] and is defined by \[\tan \theta =\dfrac{y}{x}\] . Now, replacing the things we know here into the given equation, we convert it into a simpler equation in general form of x and y and then plot it on the graph paper.

Complete step by step answer:
Now, we start off with the solution to the given problem as,
We know that \[\tan \theta =\dfrac{y}{x}\] , and from this information, we can easily find out the value of \[\sin \theta \]. The value of \[\sin \theta \] will be,
\[\sin \theta =\dfrac{y}{\sqrt{{{x}^{2}}+{{y}^{2}}}}\]
Now, we know that the value of \[r\] in this equation is given by,
\[r=\sqrt{{{x}^{2}}+{{y}^{2}}}\]
Now, replacing the above two formed equations in the given problem we get,
\[\begin{align}
  & r=4\sin \theta \\
 & \Rightarrow \sqrt{{{x}^{2}}+{{y}^{2}}}=4\dfrac{y}{\sqrt{{{x}^{2}}+{{y}^{2}}}} \\
\end{align}\]
Now, cross multiplying both the sides of the equation, we get,
\[\begin{align}
  & \Rightarrow {{x}^{2}}+{{y}^{2}}=4y \\
 & \Rightarrow {{x}^{2}}+{{y}^{2}}-4y=0 \\
\end{align}\]
Now, adding \[4\] on both the sides of the equation, we get,
\[\Rightarrow {{x}^{2}}+{{y}^{2}}-4y+4=4\]
Now, writing it in the form of a perfect square, we get,
\[\begin{align}
  & \Rightarrow {{x}^{2}}+{{\left( y-2 \right)}^{2}}=4 \\
 & \Rightarrow {{x}^{2}}+{{\left( y-2 \right)}^{2}}-4=0 \\
\end{align}\]
Plotting, it on the graph paper, we get a circle with centre \[\left( 0,2 \right)\] and radius \[2\] as the above formed equation is of the form \[{{x}^{2}}+{{y}^{2}}={{c}^{2}}\].

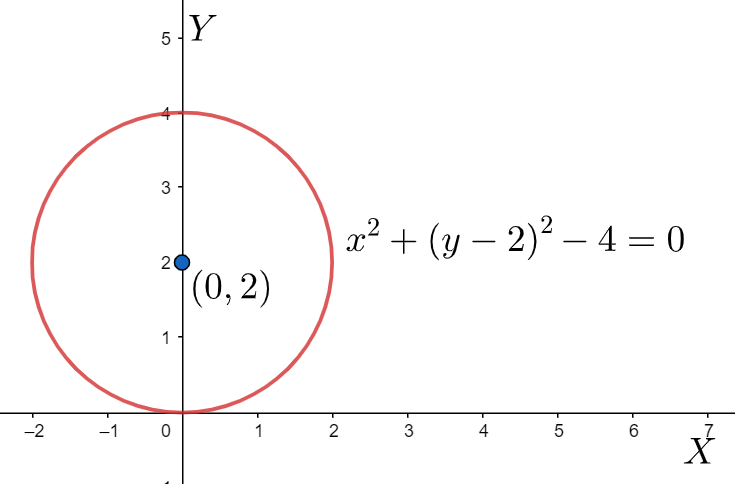
Note: For these types of problems, we need to remember the conversion from one form to another. The question is given in the polar form and we need to convert it into the general form which we are accustomed to understanding. After converting it into the general form we need to reorganise the terms so as to try to form the basic curves we know. If it falls under one of those categories, we can easily plot it with our knowledge of coordinate geometry, else we need to use derivatives and find the required points and slopes necessary for plotting a graph.