Question

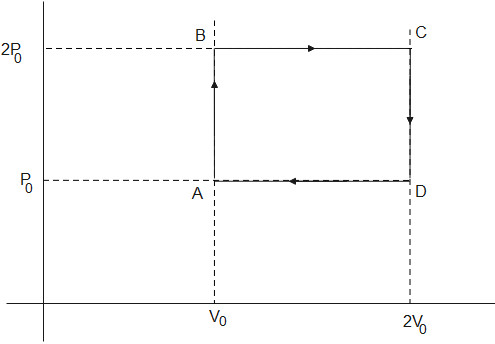
Helium gas goes through a cycle ABC (consisting of two isochoric and isobaric lines) as shown in the figure. Efficiency of this cycle is nearly: (Assume gas to be close to the ideal gas)

(A).$15.4$ %
(B). $9.1$ %
(C). $10.5$ %
(D). $12.5$ %

Answer 1

Hint: Helium is an inert gas so it’s the closest to an ideal gas. The graph depicts the working of an engine which converts the heat into work, in which heat is given to the gas and then work is done by the gas. The performance of the engine is determined through efficiency. Efficiency is the ratio of work done to the heat given.
Formulas used:
$\eta =\dfrac{W}{Q}$
$Q=n{{C}_{v}}\Delta T+n{{C}_{P}}\Delta T$

Complete answer:
Efficiency is used to analyse the performance of an engine. Efficiency is the ratio of work done by the gas to heat given to the gas. Therefore,
$\eta =\dfrac{W}{Q}$ - (1)
Here, $\eta $ is the efficiency
$W$ is the total work done by the gas
$Q$ is the total heat given to the gas


From the figure given above,
The heat given to the gas= heat given to gas from A to B at constant volume+ heat given to the gas from B to C at constant pressure
Therefore,
$Q=n{{C}_{v}}\Delta T+n{{C}_{P}}\Delta T$ - (2)
Here, $n$ is the number of moles
${{C}_{v}}$ is the specific heat at constant volume
${{C}_{P}}$ is the specific heat at constant pressure
$\Delta T$ is change in temperature
From the ideal gas equation,
$PV=nRT$
Here, $P$ is the pressure
$V$ is the volume
$R$ is the gas constant
$T$ is the temperature
From the above equation, we have,
$\Delta PV=nR\Delta T$ (at constant volume) - (3)
Using values from graph from A to B in eq (3)
$\begin{align}
  & (2{{P}_{0}}-{{P}_{0}}){{V}_{0}}=nR\Delta T \\
 & \Rightarrow \Delta T=\dfrac{{{P}_{0}}{{V}_{0}}}{nR} \\
\end{align}$
Using values from graph B to C
$\begin{align}
  & (2{{V}_{0}}){{P}_{0}}=nR\Delta T \\
 & \Rightarrow \Delta T=\dfrac{2{{P}_{0}}{{V}_{0}}}{nR} \\
\end{align}$
From monatomic gases, ${{C}_{P}}=\dfrac{5R}{2}$ and ${{C}_{V}}=\dfrac{3R}{2}$
Substituting the values in eq (2), we get,
$\begin{align}
  & Q=n{{C}_{v}}\Delta T+n{{C}_{P}}\Delta T \\
 & \Rightarrow Q=n\dfrac{3R}{2}\dfrac{{{P}_{0}}{{V}_{0}}}{nR}+n\dfrac{5R}{2}\dfrac{2{{P}_{0}}{{V}_{0}}}{nR} \\
 & \Rightarrow Q=\dfrac{3}{2}{{P}_{0}}{{V}_{0}}+5{{P}_{0}}{{V}_{0}} \\
 & \therefore Q=\dfrac{13}{2}{{P}_{0}}{{V}_{0}} \\
\end{align}$
The work done by the gas = area under the curve
$\begin{align}
  & area=l\times b \\
 & \Rightarrow area={{P}_{0}}{{V}_{0}} \\
\end{align}$
Substituting work done and heat given in eq (1), we get,
$\begin{align}
  & \eta =\dfrac{W}{Q} \\
 & \Rightarrow \eta =\dfrac{{{P}_{0}}{{V}_{0}}}{\dfrac{13}{2}{{P}_{0}}{{V}_{0}}} \\
\end{align}$
$\eqalign{
  & \Rightarrow \eta = \dfrac{2}{3} \times 100{\text{ % }} \cr
  & \therefore \eta = 15.4{\text{ % }} \cr} $
Therefore, the efficiency of the helium gas is $15.4%$.

Hence, the correct option is (A).

Note:
The carnot engine has the maximum efficiency out of all engines. The reversible engines act as refrigerators and their efficiency is calculated by the coefficient of performance. At constant pressure, the gas expands when heat is given to it and hence volume increases while at constant volume, the pressure of the gas increases.