Question

How do you graph the derivative of $f(x)=\cos (x)$?

Answer 1

Hint: In this question we will first find the derivative of the given function $f(x)$ which is equal to $\cos (x)$. We will take the derivative of the function using the formula $\dfrac{d}{dx}\cos (x)=-\sin (x)$, and then simplify the expression and plot the graph for the resultant function.

Complete step-by-step solution:
We have the given function as $f(x)=\cos (x)$. Now we have to find the derivative of the function. The derivative of the function can be taken as:
$\Rightarrow \dfrac{d}{dx}\cos (x)$
Now we know that $\dfrac{d}{dx}\cos (x)=-\sin (x)$ therefore, on using the formula in the above expression, we get:
$\Rightarrow -\sin (x)$, which is the required derivative of the function therefore, we can write it as:
$f'(x)=-\sin (x)$
Now we know the $\sin (x)$ graph starts from the origin and goes upwards and then goes downwards from the value of $\pi $ and then goes upwards again and reaches the value of $0$ again after $\pi $. It can be plotted as:

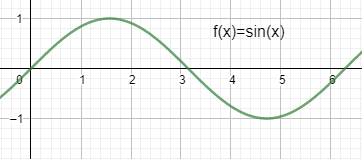
Now in this question we have to plot the graph of $-\sin (x)$. Since it is the negative graph of $\sin (x)$, the graph will have all the same values but it will be inverted. It can be plotted as:

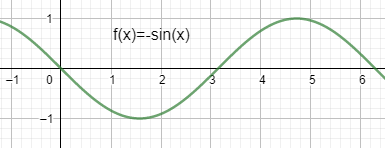
Which is the required solution.

Note: The general format of the $\sin (x)$ function should be remembered as $y=a\sin (bx+c)+d$
Where $a$ is the amplitude of the equation which tells us the maximum and the minimum value the graph would go from the base line value,
$b$ is the period of the graph,
$c$ depicts the shift of the equation, positive shift represents that the graph is shifted towards the left and negative shift represents the graph shifting to right.
And $d$ is the baseline of the equation which tells us whether the graph is going upwards or downwards.