Question

Given four distinct points in a plane. How many maximum numbers of lines can be drawn through them?
A) 6
B) 7
C) 10
D) 4

Answer 1

Hint: If there are n distinct points in a plane, then we take the help of combination to find the number of lines that can be drawn from them, by taking any two random points at a time we can find the number of lines possible.

Complete step by step solution: Given, 4 distinct points in a plane.
The number of combination, i.e., number of ways of selecting ’r’ elements out of ‘n’ is mathematically expressed as
${}^{\text{n}}{{\text{C}}_{\text{r}}}{\text{ = }}\dfrac{{{\text{n!}}}}{{{\text{r!}}\left( {{\text{n - r}}} \right){\text{!}}}}$
Now, we have given four distinct points.
Therefore, we have to find the number of ways of selecting any two points at random, mathematically i.e.,
$
  {}^{\text{4}}{{\text{C}}_{\text{2}}}{\text{ = }}\dfrac{{{\text{4!}}}}{{{\text{[(4 - 2)!](2!)}}}} \\
  {\text{ = }}\dfrac{{{\text{4!}}}}{{{\text{(2!)(2!)}}}} \\
  {\text{ = }}\dfrac{{{\text{(4)(3)(2)(1)}}}}{{{\text{(2)(1)(2)(1)}}}} \\
  {\text{ = (3)(2)}} \\
  {\text{ = 6}} \\
 $

Therefore, (A) 6 is the correct answer.

Additional information:
Combination formula helps us in finding the number of different combination like selecting ’r’ elements out of ‘n’, we use combination formula in place of finding those all combination using the formula I.e.,
${}^{\text{n}}{{\text{C}}_{\text{r}}}{\text{ = }}\dfrac{{{\text{n!}}}}{{{\text{r!}}\left( {{\text{n - r}}} \right){\text{!}}}}$

Note:

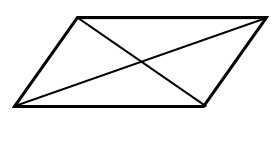
We can take the example of a quadrilateral in which we have four distinct points where there are only 6 possible lines that can be made out of those four lines i.e., four sides and two diagonals.
From the above solution, it shows ${}^{\text{4}}{{\text{C}}_{\text{2}}}{\text{ = 6}}$ and we have 6 lines joining the 4 random points shown in the above figure.