Question

Given \[\Delta ABC\] right angled at C in which AB = 29 units, BC = 21 units and \[\angle ABC=\theta \]. Find \[{{\cos }^{2}}\theta -{{\sin }^{2}}\theta \].

Answer 1

Hint:Given two sides of the right angled triangle. Find the \[{{3}^{rd}}\] side, by using basic geometry. Find the value of \[\sin \theta \] and \[\cos \theta \] from the figure. Substitute these values in \[{{\cos }^{2}}\theta -{{\sin }^{2}}\theta \] and get the value.

Complete step-by-step answer:
Consider the figure drawn,
 

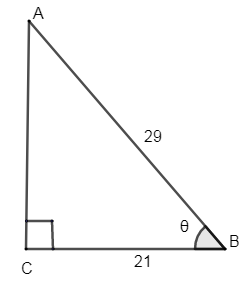
From, \[\vartriangle ABC\], AB = 29 units and BC = 21 units, \[\angle ABC=\theta \].
Using Pythagoras theorem,
\[\begin{align}
  & {{\left( Hypotenuse \right)}^{2}}={{\left( Height \right)}^{2}}+{{\left( Base \right)}^{2}} \\
 & \Rightarrow A{{B}^{2}}=A{{C}^{2}}+A{{B}^{2}} \\
 & A{{C}^{2}}=A{{B}^{2}}-B{{C}^{2}} \\
 & A{{C}^{2}}={{\left( 29 \right)}^{2}}-{{\left( 21 \right)}^{2}} \\
\end{align}\]
Using, \[{{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right)\]
\[\begin{align}
  & A{{C}^{2}}=\left( 29-21 \right)\left( 29+21 \right) \\
 & A{{C}^{2}}=8\times 50=400 \\
 & \therefore AC=\sqrt{400}=20 \\
\end{align}\]
Now, \[\sin \theta \]= \[\dfrac{Opposite side}{Hypotenuse side}\].
\[\sin \theta =\dfrac{AC}{AB}=\dfrac{20}{29}\]
\[\cos \theta \]= \[\dfrac{Adjacent side}{Hypotenuse side}\].
\[\cos \theta =\dfrac{BC}{AB}=\dfrac{21}{29}\]
We need to find the value of \[{{\cos }^{2}}\theta -{{\sin }^{2}}\theta \].
Putting values of \[\cos \theta =\dfrac{21}{29}\] and \[\sin \theta =\dfrac{20}{29}\].
\[\begin{align}
  & {{\cos }^{2}}\theta -{{\sin }^{2}}\theta ={{\left( \dfrac{21}{29} \right)}^{2}}-{{\left( \dfrac{20}{29} \right)}^{2}}=\dfrac{{{21}^{2}}-{{20}^{2}}}{{{29}^{2}}} \\
 & \because {{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right) \\
 & \Rightarrow \dfrac{\left( 21-20 \right)\left( 21+20 \right)}{{{29}^{2}}}=\dfrac{1\times 41}{{{29}^{2}}}=\dfrac{41}{841} \\
 & \therefore {{\cos }^{2}}\theta -{{\sin }^{2}}\theta =\dfrac{41}{841} \\
\end{align}\]

Note: Find altitude of the \[\Delta ABC\], which will give the values of \[\cos \theta \] and \[\sin \theta \]. Put the values in the entity to find the desired answer.Students should remember pythagoras theorem , trigonometric identities and trigonometric ratios for solving these types of problems.