Question

Give examples of two one-one functions \[{{f}_{1}}\] and \[{{f}_{2}}\] from R to R such that \[{{f}_{1}}+{{f}_{2}}:R\to R\] defined by \[\left( {{f}_{1}}+{{f}_{2}} \right)\left( x \right)={{f}_{1}}\left( x \right)+{{f}_{2}}\left( x \right)\] is not one-one.

Answer 1

Hint: For this question make \[{{f}_{1}}\left( x \right)+{{f}_{2}}\left( x \right)=\text{constant}\] as y = k is the easiest function which is not one-one. Take \[{{f}_{1}}\left( x \right)\] and \[{{f}_{2}}\left( x \right)\] as linear function in x such that \[{{f}_{1}}\left( x \right)+{{f}_{2}}\left( x \right)\] is constant.

Here we have to find two one-one functions \[{{f}_{1}}\] and \[{{f}_{2}}\] R to R such that \[\left( {{f}_{1}}+{{f}_{2}} \right)x={{f}_{1}}\left( x \right)+{{f}_{2}}\left( x \right)\] is not one-one.
We know that one-one function is a function that maps distinct elements of its domain to distinct elements of its co-domain that is for a particular value of x, there is a particular value of y and that value of y should not repeat for any other value of x.
Now, we have to make \[{{f}_{1}}\left( x \right)+{{f}_{2}}\left( x \right)\] such that it is not one-one.
We know that \[f\left( x \right)=\text{constant}\] is the easiest function which is not one-one because its value of y keeps getting repeated for all values of x.

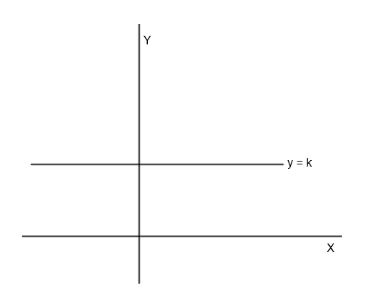
Therefore, we will choose \[{{f}_{1}}\left( x \right)\] and \[{{f}_{2}}\left( x \right)\] such that
\[{{f}_{1}}\left( x \right)+{{f}_{2}}\left( x \right)=k\]
Now, we are given that \[{{f}_{1}}\left( x \right)\] and \[{{f}_{2}}\left( x \right)\] must be one-one.
We know that the easiest one-one function is \[y=ax+b:R\to R\] where a and b are constants as it gives different values of y for different values of x.
Therefore, we take \[{{f}_{1}}\left( x \right)=9x+5\].
Now to make \[{{f}_{1}}\left( x \right)+{{f}_{2}}\left( x \right)\] constant, 9x must disappear.
Therefore, we take \[{{f}_{2}}\left( x \right)=-9x+8\].

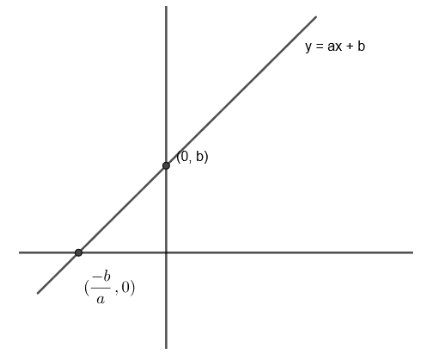
Therefore, we get \[{{f}_{1}}\left( x \right)+{{f}_{2}}\left( x \right)=\left( 9x+5 \right)+\left( -9x+8 \right)\].
\[\Rightarrow {{f}_{1}}\left( x \right)+{{f}_{2}}\left( x \right)=13\]
Therefore, finally we get
\[{{f}_{1}}\left( x \right)=9x+5\]
\[{{f}_{2}}\left( x \right)=-9x+8\]
which are one-one functions.
Also, we get \[{{f}_{1}}\left( x \right)+{{f}_{2}}\left( x \right)=13\] which is not a one-one function.

Note: Students could also check if a function is one-one or not by making the line on the graph of the function which is parallel to the x axis. If this line cuts the graph just 1 time then, it is one-one function, otherwise it is not one-one.