Question

Four solid spheres each of diameter $\sqrt{5}cm$ and mass 0.5kg are placed with their centers at the corners of the square with side 4cm. The moment of inertia of the system about the diagonal of the square is $N\times {{10}^{-4}}kg{{m}^{2}}$, then N is
a)6
b)7
c)8
d)9

Answer 1

Hint: In the question it is given to us that four spheres are placed at the corners of a square. The moment of inertia along the square along the diagonal will be due to each of the spheres. Two spheres will lie along the diagonal and the other two spheres will be separated by some distance from the diagonal of a square. Hence we will add all the moments of inertia of the four spheres with respect to the diagonal and then.
Formula used:
$I=M{{R}^{2}}$
$I(sphere)=\dfrac{2}{5}m{{r}^{2}}$

Complete answer:
Let us say there exists a solid sphere of mass ‘m’ and radius r. then the moment of inertia of the sphere about its center is given by,
$I(sphere)=\dfrac{2}{5}m{{r}^{2}}$

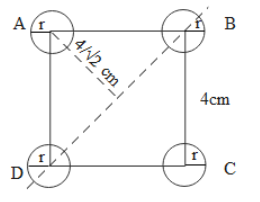
In the above figure we can see the arrangement of the spheres of mass m placed at the corners of the square of side 4cm. In the figure we can also see that there are two spheres arranged at the diagonals of the square and the remaining two at a distance $4/\sqrt{2}m$ from the diagonal. The moment of inertia along the diagonal due to the two spheres i.e. at point B and point D of the square is,
$\begin{align}
  & {{I}_{1}}=I(sphereB)+I(sphereD) \\
 & {{I}_{1}}=\dfrac{2}{5}m{{r}^{2}}+\dfrac{2}{5}m{{r}^{2}} \\
 & \Rightarrow {{I}_{1}}=\dfrac{4}{5}0.5kg{{(\dfrac{\sqrt{5}}{2}\times {{10}^{-2}})}^{2}} \\
 & \Rightarrow {{I}_{1}}=0.5\times {{10}^{-4}}kg{{m}^{2}}=0.5\times {{10}^{-4}}kg{{m}^{2}} \\
\end{align}$
The spheres at corners C and A are at a distance of $4/\sqrt{2}m$cm from the diagonal. According to parallel axis theorem, the moment of inertia ${{I}_{B}}$ of a body at a distance of d from the axis through of centre of mass is equal to the sum of moment of inertia along the axis through the centre of mass and mass of the body(M) times square of the distance from centre of mass. Mathematically written as,
${{I}_{B}}={{I}_{CM}}+M{{d}^{2}}$
Hence by parallel axis theorem, the moment of inertia(${{I}_{2}}$ ) along the diagonal due to the two spheres at A and C is,
$\begin{align}
  & {{I}_{2}}=I(sphereA)+I(sphereC) \\
 & \Rightarrow {{I}_{2}}={{I}_{CM}}+M{{d}^{2}}+{{I}_{CM}}+M{{d}^{2}} \\
 & \Rightarrow {{I}_{2}}=2({{I}_{CM}}+M{{d}^{2}}) \\
 & \Rightarrow {{I}_{2}}=2(\dfrac{2}{5}m{{r}^{2}}+M{{d}^{2}}) \\
 & \Rightarrow {{I}_{2}}=\dfrac{4}{5}0.5kg{{(\dfrac{\sqrt{5}}{2}\times {{10}^{-2}}m)}^{2}}+2\times 0.5kg{{\left( \dfrac{4}{\sqrt{2}}\times {{10}^{-2}} \right)}^{2}} \\
 & \Rightarrow {{I}_{2}}=0.5\times {{10}^{-4}}+{{\left( \dfrac{4}{\sqrt{2}}\times {{10}^{-2}} \right)}^{2}} \\
 & \Rightarrow {{I}_{2}}=0.5\times {{10}^{-4}}+8\times {{10}^{-4}}=8.5\times {{10}^{-4}}kg{{m}^{2}} \\
\end{align}$
Hence the total moment of inertia($I$) of the body along the diagonal of the square is,
$\begin{align}
  & I={{I}_{1}}+{{I}_{2}} \\
 & \Rightarrow I=0.5\times {{10}^{-4}}kg{{m}^{2}}+8.5\times {{10}^{-4}}kg{{m}^{2}} \\
 & \Rightarrow I=9\times {{10}^{-4}}kg{{m}^{2}} \\
\end{align}$
$N\times {{10}^{-4}}kg{{m}^{2}}$if we compare the adjacent equation and the above answer obtained we get the value of N as 9.

Hence the correct answer of the above question is option d.

Note:
It is to be noted that if there exists a system arrangement where the particles of the system itself have a moment of inertia, then we have to consider their individual moment of inertia. The parallel axis theorem usually comes to help in such cases. If the particles lie on the axis itself, then the moment of inertia along the axis will also be due to the moment of inertia of the particles about their center of mass.