Question

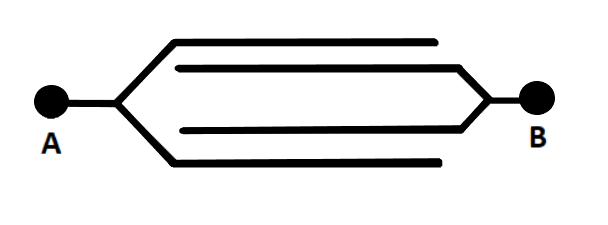
Four metallic plates each with surface area of one side $ A $ , are placed at a distance $ d $ from each other. The two outer plates are connected to one point $ A $ and the two other inner plates to another point $ B $ as shown in the figure. Then the capacitance of the system is:

(A) $ \dfrac{{{\varepsilon _0}A}}{d} $
(B) $ \dfrac{{2{\varepsilon _0}A}}{d} $
(C) $ \dfrac{{3{\varepsilon _0}A}}{d} $
(D) $ \dfrac{{4{\varepsilon _0}A}}{d} $

Answer 1

Hint :Capacitance is defined as the ability of plates to store energy when there will be potential difference between the plates. Here, the plates will form three capacitors when they are connected to each other. Therefore, to calculate the capacitance of the system, we will add the capacitance of each capacitor.
The formula of capacitance of each plate is given by
 $ C = \dfrac{{{\varepsilon _0}A}}{d} $
Here, $ C $ is the capacitance, $ {\varepsilon _0} $ is the permittivity, $ A $ is the area of plates and $ d $ is the separation between the plates.

Complete Step By Step Answer:
Four metallic plates are connected with each other. These plates are connected in such a way they will form three capacitors, each of them will have a potential difference $ AB $ .
Now, when the capacitors will have the same potential difference, then the capacitor is said to be a parallel combination.
Now, capacitance is defined as the ability of plates to store energy when there will be potential difference between the plates. The capacitance in the plates of area $ A $ separated by a distance $ d $ from each other is given by
 $ C = \dfrac{{{\varepsilon _0}A}}{d} $
Now, as the plates are forming three capacitors having potential difference $ AB $ , therefore, to calculate the capacitance of the system, we will calculate the capacitance of each three plate as shown below
 $ {C_{net}} = \dfrac{{{\varepsilon _0}A}}{d} + \dfrac{{{\varepsilon _0}A}}{d} + \dfrac{{{\varepsilon _0}A}}{d} $
 $ \Rightarrow {C_{net}} = \dfrac{{3{\varepsilon _0}A}}{d} $
Therefore, the capacitance of the system consisting of four plates is $ \dfrac{{3{\varepsilon _0}A}}{d} $
Hence, option (C) is the correct option.

Note :
We can also calculate the capacitance of the system of four plates as shown below
 $ {C_{net}} = 3C $
 $ \Rightarrow \,{C_{net}} = \dfrac{{3{\varepsilon _0}A}}{d} $
The result is the same as that of the result calculated above. We have multiplied the capacitance by $ 3 $ because the plates are forming the combination of three capacitors.