Question

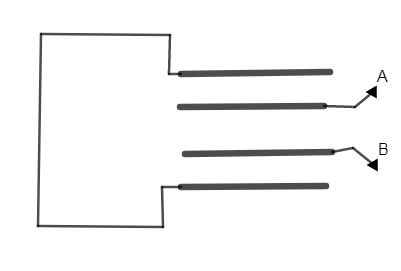
Four metallic plates each with a surface area of A are placed at a distance from each other. The plates are connected as shown in the circuit diagram. Then the capacitance of the system between a and b is-

\[\begin{align}
  & A.\text{ }\dfrac{3{{\varepsilon }_{o}}A}{d} \\
 & B.\text{ }\dfrac{2{{\varepsilon }_{o}}A}{d} \\
 & C.\text{ }\dfrac{2{{\varepsilon }_{o}}A}{3d} \\
 & D.\text{ }\dfrac{3{{\varepsilon }_{o}}A}{2d} \\
\end{align}\]

Answer 1

Hint: It is given in the question that the four metallic plates each with a surface area of A placed at a distance d from each other and we have to find the capacitance between point a and b to do so we have to simplify the given figure and check which the capacitor is parallel to the each other and which one is in series and by using formula of the capacitance we can get total capacitance of the given system.
Formula used:
$C=\dfrac{{{\varepsilon }_{o}}A}{d}$

Complete answer:
In order to find a solution we have to simplify the circuit by making all four plates by 1, 2, 3, and 4 as shown in the figure.

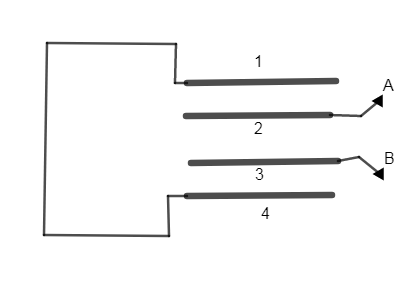
Now to further simplify the circuit we will write points step by step and then we will draw full circuit.
Now ‘a’ is connected with the plate 2 which is in connection with the plate 1 and the plate 3, therefore capacitor 21 and 23 will be in parallel connection.
Now plate 1 is connected to plate 4 which is making a capacitor with plate 3 therefore the capacitor 21 and 43 will be in the series connection.
Now the capacitor with the plate 23 and the plate 43 has common plate 3 which is connected to b.
Now let’s make the figure according to our simplification.

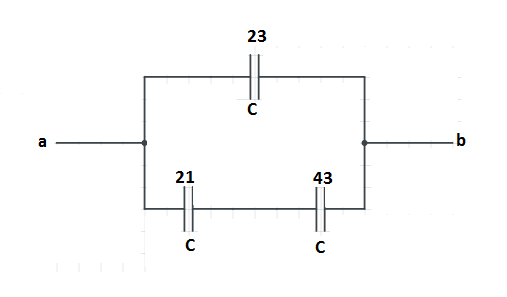
Now the total capacitance of the capacitor which are connected in series is,
Note that all have the same capacitance ‘c’ because their area and the distance are same.
$\begin{align}
  & \dfrac{1}{{{C}_{1}}}=\dfrac{1}{C}+\dfrac{1}{C}\text{ }\left( \text{for the plate }\!\!'\!\!\text{ 21 }\!\!'\!\!\text{ and }\!\!'\!\!\text{ 43 }\!\!'\!\!\text{ } \right) \\
 & \dfrac{1}{{{C}_{1}}}=\dfrac{2C}{{{C}^{2}}} \\
 & \therefore {{C}_{1}}=\dfrac{C}{2}....\left( 1 \right) \\
\end{align}$
Now the total capacitance,
$\begin{align}
  & {{C}_{T}}=C+\dfrac{C}{2} \\
 & {{C}_{T}}=\dfrac{3C}{2}...\left( 2 \right) \\
\end{align}$
Now we know that formula for the capacitor is,
$C=\dfrac{{{\varepsilon }_{o}}A}{d}$
$C=\dfrac{{{\varepsilon }_{o}}A}{d}$
Where, ${{\varepsilon }_{o}}$ = permittivity
A = area
d = distance between the two conductive plate,
Now substitute value of the equation (3) in the equation (2)
$\begin{align}
  & {{C}_{T}}=\dfrac{3}{2}\times \dfrac{{{\varepsilon }_{o}}A}{d} \\
 & {{C}_{T}}=\dfrac{3{{\varepsilon }_{o}}A}{2d} \\
\end{align}$

Therefore the option (D) is correct.

Note:
While calculating capacitance of the parallel circuit and the series circuit be careful while putting the formulas of the series and parallel connection because sometimes we can be mistaken formulas as we are using formulas resistance formula i.e.
Series connection,
Resistance,
${{R}_{e}}={{R}_{1}}+{{R}_{2}}+{{R}_{3}}....$
Capacitor,
$\dfrac{1}{{{C}_{e}}}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}+\dfrac{1}{{{C}_{3}}}....$
Parallel connection,
Resistance,
$\dfrac{1}{{{R}_{e}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}......$
Capacitor,
${{C}_{e}}={{C}_{1}}+{{C}_{2}}+{{C}_{3}}.....$