Question

How do you find the \[x\] and \[y\] intercepts for \[y=2{{x}^{3}}+3x-5\]?

Answer 1

Hint: \[x\] and \[y\] intercepts for the given expression can be found by keeping one of the variables as zero. That is, to find the x intercept, the point at which the equation intersects the x-axis, we will have to keep \[y=0\] and to find the y intercept, the point at which the equation intersects the y-axis, we will have to keep the \[x=0\].

Complete step-by-step solution:
x- intercept refers to the point in the graph of a given equation which intersects the x-axis. At that point, y-coordinate will be zero. This information is important to find the x-intercept else we will have to draw the graph of the given equation.
Similarly, y- intercept refers to the point in the graph of a given equation which intersects the y-axis. At that point, x coordinate will be zero. This information is important to find the y-intercept else we will have to draw the graph of the given equation. We will verify our answer with the help of a graph at the end.
According to the given question, we are to find the \[x\] and \[y\] intercepts for \[y=2{{x}^{3}}+3x-5\],
Let’s start with finding x-intercept,
We will take \[y=0\]
So the equation gets the form,
\[2{{x}^{3}}+3x-5=0\]
Now solving the equation for the value of \[x\], since the degree of the polynomial is 3, we will get three values of \[x\].
\[\Rightarrow 2{{x}^{3}}+3x=5\]
Taking \[x\] common, we get
\[\Rightarrow x(2{{x}^{2}}+3)=5\]
We have \[x=5\] and \[2{{x}^{2}}+3=5\]
So, one value of \[x=5\], since it does not satisfy the equation it is removed, solving other part,
\[2{{x}^{2}}+3=5\]
\[\Rightarrow 2{{x}^{2}}=2\]
\[\Rightarrow {{x}^{2}}=1\]
\[x=\pm 1\]
Since, \[x=-1\]does not satisfy the equation it is removed as well.
Now, we only have \[x=1\]
So, we get the value of x-intercept in the equation: \[(1,0)\]
Now, let’s find the y-intercept,
We will take \[x=0\], we get the equation as
\[y=2(0)+3(0)-5\]
\[y=-5\]
So, the y-intercept is \[(0,-5)\].

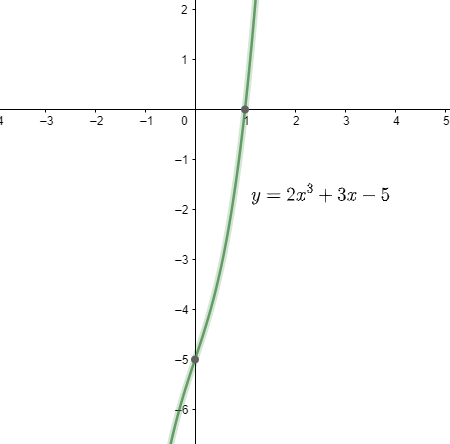
Therefore, the \[x\] and \[y\] intercepts for \[y=2{{x}^{3}}+3x-5\] are:
 x-intercept in the equation is \[(1,0)\]
 y-intercept is \[(0,-5)\]

Note: \[x\] and \[y\] intercept are found by taking \[y=0\] and \[x=0\] respectively. It should be kept in mind while doing the calculation and not interpreted the other way round. Also while substituting the values of \[x\] and \[y\], it should be calculated carefully else will result in a wrong answer.