Question

How to find the values of \[p\] for which demand is elastic and the values for which demand is inelastic, with the price demand equation as \[f\left( p \right) = 455 - 35p\]?

Answer 1

Hint: Here, we will find the demand at which the price vanishes and the price at which the demand vanishes which are the \[x\]-intercepts and \[y\]-intercepts. We will plot the demand curve by using the extreme points. We will then use the midpoint formula to find the midpoint of the demand curve. By simplifying the equation, we will find the values for which demand is elastic and is inelastic.

Formula Used:
Midpoint Formula \[ = \left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)\]

Complete Step by Step Solution:
We are given a function \[f\left( p \right) = 455 - 35p\].
The given equation is a linear equation.
Let \[p\] be the Price and \[f\left( p \right)\] be the Price Demand Equation. Let the Price Demand equation \[f\left( p \right)\] be\[x\]
Thus, we get \[x = 455 - 35p\].
Now, we will find the Demand at which the Price vanishes by substituting \[p = 0\] in the above equation.
\[ \Rightarrow x = 455 - 35\left( 0 \right)\]
Now, by simplifying, we get
\[ \Rightarrow x = 455\]
At the Demand \[x = 455\], the price vanishes.
Now, we will find the Price at which the Demand vanishes by substituting \[x = 0\] in the equation \[x = 455 - 35p\]. Therefore, we get
\[0 = 455 - 35p\]
Subtracting 455 from both the sides, we get
\[ \Rightarrow - 35p = - 455\]
Dividing both sides by \[ - 35\], we get
\[ \Rightarrow p = \dfrac{{ - 455}}{{ - 35}}\]
\[ \Rightarrow p = 13\]
At the Price \[p = 13\], the demand vanishes.
Thus, the two extreme points are\[\left( {0,13} \right)\] and \[\left( {455,0} \right)\].
Now, we will plot the graph for the two extreme points which is a demand curve for the price demand equation

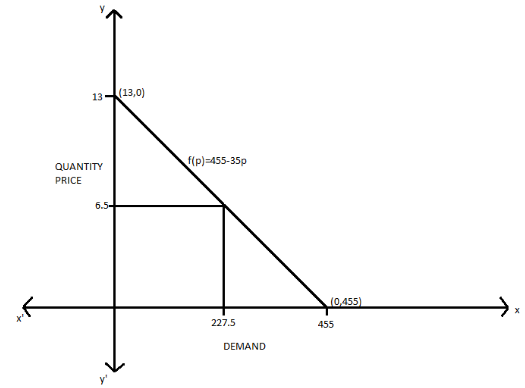
Now, we will find the midpoint of the demand equation, by using the midpoint formula
Midpoint Formula \[ = \left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)\]
Now, by using the two extreme points \[\left( {0,13} \right)\] and \[\left( {455,0} \right)\] of the demand curve, we get
\[ \Rightarrow \] Midpoint of the demand \[ = \left( {\dfrac{{0 + 455}}{2},\dfrac{{13 + 0}}{2}} \right)\]
\[ \Rightarrow \] Midpoint of the demand \[ = \left( {\dfrac{{455}}{2},\dfrac{{13}}{2}} \right)\]
Dividing the terms, we get
\[ \Rightarrow \] Midpoint of the demand \[ = \left( {227.5,6.5} \right)\]
Thus, at price \[6.5\] , the quantity demanded is \[227.5\].
Exactly at the middle of the demand equation, the length of the lower segment is equal to the length of the upper segment in the demand curve. Hence the elasticity at the midpoint of the demand curve is unitary.
We know that the Demand is relatively inelastic in the lower segment of the demand curve and Demand is relatively elastic in the upper segment of the demand curve.
Therefore, Demand is relatively elastic for any price greater than \[6.5\] and Demand is relatively inelastic for any price lesser than \[6.5\].

Note:
We know that Price elasticity is defined as the ratio of change in quantity demanded or supplied to the change in price. Price Elasticity is of three types: Elastic, Inelastic or Unitary. Elastic Demand is defined as the ratio of change in quantity demanded to the change in price which is greater than the proportion. Inelastic Demand is defined as the ratio of change in quantity demanded to the change in price which is less than the proportion. Demand curve gives the curve for the demand and the price. The given demand equation forms a linear demand curve.