Question

How do you find the slope and intercept of $x + y = 9$?

Answer 1

Hint:In order to determine the slope and intercept to the above equation first rewrite the equation in such a way that the left side of the equation contain only variable $y$ , $y = - x + 9$ and compare with the slope-intercept form $y = mx + c$, m is the slope and c is the y-intercept.

Complete step by step solution:
We are given a linear equation in two variables $x\, and \,y$ i.e. $x + y = 9$
Rewriting the above equation such that the left-hand side of the equation contains only variable $y$.
$x + y = 9$
Transposing the term having variable $x$ to the RHS, we get
$y = - x + 9$
To determine the slope and intercept of the above equation comparing it with the slope-intercept form $y = mx + c$
Where, m is the slope and c is the y-intercept.
$y = - x + 9$ comparing with slope-intercept form $y = mx + c$
So $
m = - 1 \\
c = 9 \\
$
Let's graph the equation, we are jumping on the cartesian plane.
There is one most important property of a plane that graphs the equation of form $ax + by + c = 0$ is always a straight line.
Graph of equation having y-intercept as $(0,9)$with slope $m = - 1$

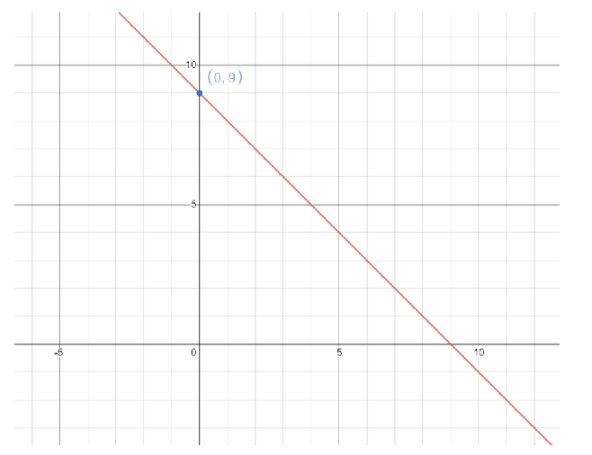
Hence we’ve successfully plotted graph of $x + y = 9$
Therefore, the slope and intercept to the expression$x + y = 9$ is equal to $ - 1\,\,and\,\,9$ respectively.

Additional Information:
1. Cartesian Plane: A Cartesian Plane is given its name by the French mathematician Rene Descartes ,who first used this plane in the field of mathematics .It is defined as the two mutually perpendicular number line , the one which is horizontal is given name x-axis and the one which is vertical is known as y-axis. With the help of these axes we can plot any point on this cartesian plane with the help of an ordered pair of numbers.
2.Slope-Intercept Form= $y = mx + c$

Note:
1.Draw the cartesian plane only with the help of a straight ruler and pencil to get the perfect and accurate results.
2.Slope of line perpendicular to the line having slope $m$is equal to $ - \dfrac{1}{m}$.