Question

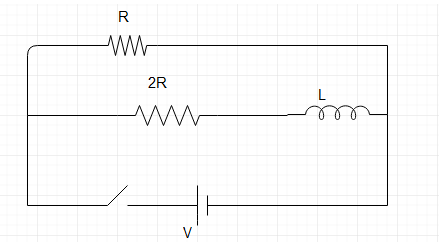
Find the ratio of time constant in build up and decay in the circuit as shown in the flowing figure-

A. 1:1
B. 3:2
C. 2:3
D. 1:3

Answer 1

Hint: The time constant for an RL circuit shows us the amount of time the circuit takes to conduct 63.2% of the current that flows on account of potential difference applied to its end. The formula of time constant is \[T=\dfrac{L}{R}\]. The current flowing through a conductor does not change spontaneously but with the passage of time.

Complete step by step answer:
The inductor, L is in series with the resistance 2R in the second branch of the given circuit. So, the Time constant in Build up is given as \[{{T}_{1}}=\dfrac{L}{2R}\].
Now talking about decay, time constant is given by, \[{{T}_{2}}=\dfrac{L}{3R}\]
So, taking the ratio of the two time constants we get, \[\dfrac{{{T}_{1}}}{{{T}_{2}}}=\dfrac{2}{3}\]
So, the correct option is (b)

Note:Inductor always opposes the flow of current through it. An ideal inductor pays no opposition to the flow of current but in reality, no ideal inductor exists. When current flows through the inductor it changes and self-induced emf within the inductor as a result of the growth of magnetic flux, (Lenz’s Law) is produced which opposes the cause of its growth. As the time goes on, external potential neutralizes the effect of the self-induced emf, the current flow becomes constant and the induced current and field are reduced to zero. The Time Constant of the LR series circuit represents the final steady state current value after five-time constant values.