
Find the position of centre of mass of the quarter solid sphere from $C$ in which mass per unit volume is given as $\rho (r)={{\rho }_{o}}\left( 1-\dfrac{r}{R} \right)$, where $r$ is the radial distance from centre and $R$ is the radius of solid quarter sphere.
$A.\dfrac{3}{10}R$
$B.\dfrac{3\sqrt{2}}{7}R$
$C.\dfrac{3\sqrt{2}}{10}R$
$D.\dfrac{3\sqrt{2}}{5}R$

Answer
561k+ views
Hint: We know that Centre of mass of a body is defined as the point at which the distribution of mass is equal in all directions. We will use the formula of centre of mass symmetric to the y-axis to solve the given problem. Method of integration is used to solve the problem.
Formula Used:
We are going to use the following formula to solve the problem:-
${{y}_{cm}}=\dfrac{\int\limits_{0}^{R}{\left[ {{\rho }_{o}}\left( 1-\dfrac{r}{R} \right)2\pi {{r}^{2}}dr \right]\dfrac{r}{2}}}{\int\limits_{0}^{R}{\left[ {{\rho }_{o}}\left( 1-\dfrac{r}{R} \right)2\pi {{r}^{2}}dr \right]}}$
Complete answer:
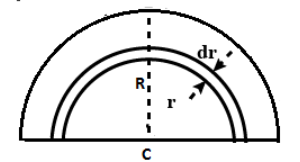
From the figure we cut an element of length $dr$. We know that the centre of mass is calculated by dividing the sum of product of mass moment of inertia and the mean distance by the sum of areas. In this case we have to integrate it to find the whole solid in terms of an element. We have the following parameters with us:-
Mass per unit volume is given as $\rho (r)={{\rho }_{o}}\left( 1-\dfrac{r}{R} \right)$, where $r$ is the radial distance from centre, $R$ is the radius of solid quarter sphere and position of centre of mass of the quarter solid sphere is ${{y}_{cm}}$ .
Area of the cross section is given as $2\pi {{r}^{2}}dr$ and mean distance as $\dfrac{r}{2}$. Now, using following formula we have:-
${{y}_{cm}}=\dfrac{\int\limits_{0}^{R}{\left[ {{\rho }_{o}}\left( 1-\dfrac{r}{R} \right)2\pi {{r}^{2}}dr \right]\dfrac{r}{2}}}{\int\limits_{0}^{R}{\left[ {{\rho }_{o}}\left( 1-\dfrac{r}{R} \right)2\pi {{r}^{2}}dr \right]}}$
$\Rightarrow {{y}_{cm}}=\dfrac{\dfrac{2\pi {{\rho }_{o}}}{2}\int\limits_{0}^{R}{\left[ \left( \dfrac{R-r}{R} \right){{r}^{2}}dr \right]r}}{2\pi {{\rho }_{o}}\int\limits_{0}^{R}{\left[ \left( \dfrac{R-r}{R} \right){{r}^{2}}dr \right]}}$
Integrating further and solving we get,
${{y}_{cm}}=\dfrac{\dfrac{1}{2}\left( \dfrac{{{R}^{4}}}{4}-\dfrac{{{R}^{5}}}{5R} \right)}{\left( \dfrac{{{R}^{3}}}{3}-\dfrac{{{R}^{4}}}{4R} \right)}$
Solving further we get,
${{y}_{cm}}=\dfrac{3}{10}R$
Hence, option $(A)$ is correct.
Note:
We should be clear about our concept of centre of mass and centre of gravity. Different bodies with different geometric shapes have different points as the centre of mass. Centre of mass does not depend on the gravitational field but the centre of gravity does depend on the gravitational field. Centre of mass and centre of gravity of a body in a uniform gravitational field are always equal but they may be at different points if the gravitational field is not uniform.
Formula Used:
We are going to use the following formula to solve the problem:-
${{y}_{cm}}=\dfrac{\int\limits_{0}^{R}{\left[ {{\rho }_{o}}\left( 1-\dfrac{r}{R} \right)2\pi {{r}^{2}}dr \right]\dfrac{r}{2}}}{\int\limits_{0}^{R}{\left[ {{\rho }_{o}}\left( 1-\dfrac{r}{R} \right)2\pi {{r}^{2}}dr \right]}}$
Complete answer:

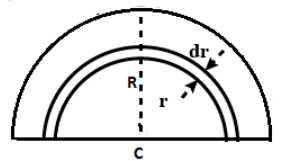
From the figure we cut an element of length $dr$. We know that the centre of mass is calculated by dividing the sum of product of mass moment of inertia and the mean distance by the sum of areas. In this case we have to integrate it to find the whole solid in terms of an element. We have the following parameters with us:-
Mass per unit volume is given as $\rho (r)={{\rho }_{o}}\left( 1-\dfrac{r}{R} \right)$, where $r$ is the radial distance from centre, $R$ is the radius of solid quarter sphere and position of centre of mass of the quarter solid sphere is ${{y}_{cm}}$ .
Area of the cross section is given as $2\pi {{r}^{2}}dr$ and mean distance as $\dfrac{r}{2}$. Now, using following formula we have:-
${{y}_{cm}}=\dfrac{\int\limits_{0}^{R}{\left[ {{\rho }_{o}}\left( 1-\dfrac{r}{R} \right)2\pi {{r}^{2}}dr \right]\dfrac{r}{2}}}{\int\limits_{0}^{R}{\left[ {{\rho }_{o}}\left( 1-\dfrac{r}{R} \right)2\pi {{r}^{2}}dr \right]}}$
$\Rightarrow {{y}_{cm}}=\dfrac{\dfrac{2\pi {{\rho }_{o}}}{2}\int\limits_{0}^{R}{\left[ \left( \dfrac{R-r}{R} \right){{r}^{2}}dr \right]r}}{2\pi {{\rho }_{o}}\int\limits_{0}^{R}{\left[ \left( \dfrac{R-r}{R} \right){{r}^{2}}dr \right]}}$
Integrating further and solving we get,
${{y}_{cm}}=\dfrac{\dfrac{1}{2}\left( \dfrac{{{R}^{4}}}{4}-\dfrac{{{R}^{5}}}{5R} \right)}{\left( \dfrac{{{R}^{3}}}{3}-\dfrac{{{R}^{4}}}{4R} \right)}$
Solving further we get,
${{y}_{cm}}=\dfrac{3}{10}R$
Hence, option $(A)$ is correct.
Note:
We should be clear about our concept of centre of mass and centre of gravity. Different bodies with different geometric shapes have different points as the centre of mass. Centre of mass does not depend on the gravitational field but the centre of gravity does depend on the gravitational field. Centre of mass and centre of gravity of a body in a uniform gravitational field are always equal but they may be at different points if the gravitational field is not uniform.
Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




