Question

Find the points which divide the line segment joining $ (8,12) $ and $ (12,8) $ into four equal parts.

Answer 1

Hint: Draw a rough sketch of a line joining the coordinates $ (8,12) $ and $ (12,8) $ . Then mark the four points on the line segment, assuming that they divide the line segment into four equal parts. Then use the property of the coordinate of midpoint, to find the coordinate of all the three points.

Complete step-by-step answer:
Observe the diagram

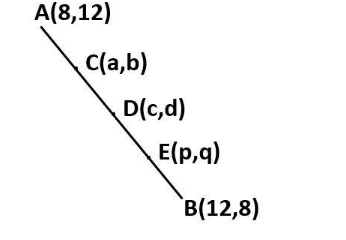
Let $ A(8,12) $ and $ B(12,8) $ be the two given points.
Let $ C(a,b),D(b,c),E(p,q) $ be the three points that divide the line AB into four equal parts.
By observing the diagram, we can conclude that D must be the midpoint AB.
Then by the property of mid-point, the coordinates of D can be given as
 $ c = \dfrac{{8 + 12}}{2} $ and $ d = \dfrac{{12 + 8}}{2} $
 $ \Rightarrow c = \dfrac{{20}}{2} = 10 $ and $ d = \dfrac{{20}}{2} = 10 $
Thus, the coordinate of D are $ (10,10) $
Again, by observing the diagram, we can say that, C is the midpoint of AD
Then by the property of mid-point, the coordinates of C can be given as
 $ a = \dfrac{{8 + 10}}{2} $ and $ b = \dfrac{{12 + 10}}{2} $
 $ \Rightarrow a = \dfrac{{18}}{2} = 9 $ and $ b = \dfrac{{22}}{2} = 11 $
Thus, the coordinates of C are $ (9,11) $
Now, by again observing the diagram, we can say that E is the midpoint of DB.
Then by the property of mid-point, the coordinates of E can be given as
 $ p = \dfrac{{10 + 12}}{2} $ and $ q = \dfrac{{10 + 8}}{2} $
 $ \Rightarrow p = \dfrac{{22}}{2} = 11 $ and $ q = \dfrac{{18}}{2} = 9 $
Thus, the coordinates of E are $ (11,9) $
Hence, the points which divide the line segment $ (8,12) $ and $ (12,8) $ are $ (9,11),(10,10),(11,9) $
So, the correct answer is “(9,11),(10,10),(11,9)”.

Note: If it doesn’t click to use the mid-point theorem then this question can also be solved by using, section formula. We can say that the point C divides AB in the ratio $ 1:4 $ . Then find the value of C using section formula. And then repeat the same concept for finding other points as well. But knowing mid-point property will help solve this question easily and in a less number of steps.