Question

Find the point on the parabola \[{y^2} = 4ax\] , (a>0) which forms a triangle of area \[3{a^2}\] with the vertex and focus of the parabola.

Answer 1

Hint: In this particular problem, express the point on parabola in parametric form and form a triangle using the vertex and the focus and that point. Thus, find the area of the triangle and equate to the given area to find the unknown coordinates.

Complete step-by-step answer:
Let the point on the parabola \[{y^2} = 4ax\] be P.
So, we had to express P on parabola \[{y^2} = 4ax\] in parametric form
\[ \Rightarrow \]So, \[P \equiv \left( {a{t^2},2at} \right)\]

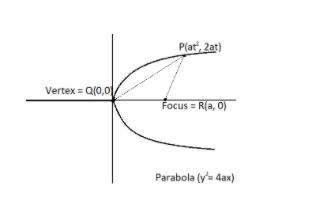
Now as we can see from the above figure that Q is the vertex of the given parabola.
\[ \Rightarrow \]So, \[Q \equiv \left( {0,0} \right)\]
And, R be the focus of the parabola \[{y^2} = 4ax\]
\[ \Rightarrow \]So, \[R \equiv \left( {a,0} \right)\]
Now as we know that if we are given with the coordinates of three points as \[A\left( {u,v} \right)\], \[B\left( {w,x} \right)\] and \[C\left( {y,z} \right)\]. Then, the area of the triangle ABC will be equal to \[\begin{gathered}
  \dfrac{1}{2}\left| {\begin{array}{*{20}{c}}
  u&v&1 \\
  w&x&1 \\
  y&z&1
\end{array}} \right| \\
    \\
\end{gathered} \].
So, the area of the triangle with coordinates as \[P \equiv \left( {a{t^2},2at} \right)\], \[Q \equiv \left( {0,0} \right)\] and \[R \equiv \left( {a,0} \right)\].
So, the area of the triangle will be equal to \[\dfrac{1}{2}\left| {\begin{array}{*{20}{c}}
  {a{t^2}}&{2at}&1 \\
  0&0&1 \\
  a&0&1
\end{array}} \right|\]
Area = \[\dfrac{1}{2}\left[ {a{t^2}\left( {0 \times 1 - 1 \times 0} \right) - 2at\left( {0 \times 1 - 1 \times a} \right) + 1\left( {0 \times 0 - 0 \times a} \right)} \right] = \dfrac{1}{2}\left[ {2{a^2}t} \right] = {a^2}t\]
Now as we know that we are given in the question that the area of the triangle formed by joining focus vertex and a point on parabola (i.e. PQR) is equal to \[3{a^2}\].
So, \[3{a^2} = {a^2}t\]
Therefore, t = 3
So, coordinates of point P will be \[P \equiv \left( {a{{\left( 3 \right)}^2},2a\left( 3 \right)} \right) \equiv \left( {9a,6a} \right)\]
Hence, the coordinates of the point which forms a triangle of area \[3{a^2}\] with vertex and focus of the parabola \[{y^2} = 4ax\] will be \[\left( {9a,6a} \right)\].

Note: Whenever we face such questions then the key concept is to recall the parametric coordinates of the parabola. Ans assume the coordinates of the point in parametric form. And then find the area of the triangle formed by using determinant (as stated above). And then equate that area with the given area to find the value of t. And then put the value of t in parametric coordinates to find the coordinates of that point. This will be the easiest and efficient way to find the solution of the problem.