Question

How do you find the parametric equation of a parabola?

Answer 1

Hint: In this question, we have to find the parametric equation of a parabola. As we know, a parabola is a symmetrical plane or a curve that is formed by the intersection of the cone with a plane parallel to its side. Also, a parametric equation is a type of equation that employs an independent variable called a parameter and in which dependent variables are continuous functions of the parameter. Therefore, in this problem, we have to find the parametric equation of the parabola.

Complete step-by-step solution:
According to the question, we have to find the parametric equation of a parabola. A parabola is a symmetrical plane that is formed by the intersection of the cone with a plane parallel to its side.
So, we will solve four different cases of the parabola.
Case 1: Now, we know the standard equation of the parabola is ${{y}^{2}}=-4ax$ ----- (1)
Therefore, the graph of the equation ${{y}^{2}}=-4ax$ is as follows:

Now, we will let $x=-a{{t}^{2}}$ and $y=2at$ , and put the value of x and y in the equation (1), we get
${{\left( 2at \right)}^{2}}=-4a\left( -a{{t}^{2}} \right)$
On further solving, we get
\[4{{a}^{2}}{{t}^{2}}=4{{a}^{2}}{{t}^{2}}\]
Thus, we see that both the LHS and RHS are equal to each other, which implies for the parabolic equation ${{y}^{2}}=-4ax$ , its parametric equations are $x=-a{{t}^{2}}$ and $y=2at$.
Case 2: Now, we know the standard equation of the parabola is ${{y}^{2}}=4ax$ ----- (2)
Therefore, the graph of the equation ${{y}^{2}}=4ax$ is as follows:

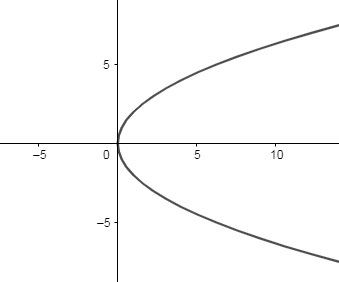
Now, we will let $x=a{{t}^{2}}$ and $y=2at$ , and put the value of x and y in the equation (2), we get
${{\left( 2at \right)}^{2}}=4a\left( a{{t}^{2}} \right)$
On further solving, we get
\[4{{a}^{2}}{{t}^{2}}=4{{a}^{2}}{{t}^{2}}\]
Thus, we see that both the LHS and RHS are equal to each other, which implies for the parabolic equation ${{y}^{2}}=4ax$ , its parametric equations are $x=a{{t}^{2}}$ and $y=2at$.
Case 3: Now, we know the standard equation of the parabola is ${{x}^{2}}=4ay$ ----- (3)
Therefore, the graph of the equation ${{x}^{2}}=4ay$ is as follows:

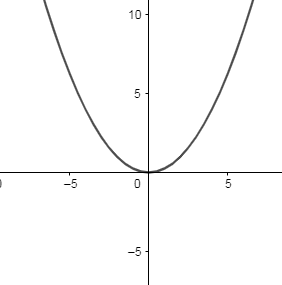
Now, we will let $x=2at$ and $y=a{{t}^{2}}$ , and put the value of x and y in the equation (3), we get
${{\left( 2at \right)}^{2}}=4a\left( a{{t}^{2}} \right)$
On further solving, we get
\[4{{a}^{2}}{{t}^{2}}=4{{a}^{2}}{{t}^{2}}\]
Thus, we see that both the LHS and RHS are equal to each other, which implies for the parabolic equation ${{x}^{2}}=4ay$ , its parametric equations are $x=2at$ and $y=a{{t}^{2}}$.
Case 4: Now, we know the standard equation of the parabola is ${{x}^{2}}=-4ay$ ----- (4)
Therefore, the graph of the equation ${{x}^{2}}=-4ay$ is as follows:

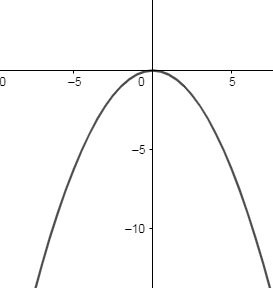
Now, we will let $x=2at$ and $y=-a{{t}^{2}}$ , and put the value of x and y in the equation (4), we get
${{\left( 2at \right)}^{2}}=-4a\left( -a{{t}^{2}} \right)$
On further solving, we get
\[4{{a}^{2}}{{t}^{2}}=4{{a}^{2}}{{t}^{2}}\]
Thus, we see that both the LHS and RHS are equal to each other, which implies for the parabolic equation ${{x}^{2}}=-4ay$ , its parametric equations are $x=2at$ and $y=-a{{t}^{2}}$.
Therefore, we have found the 4 parametric equations of the parabola.

Note: While solving this problem, do mention all the steps properly to avoid confusion and mathematical error. Do to forget the standard form of the equation of the parabola. Also, do all the four cases, to get the required result for the solution.