Question

Find the maximum area of an isosceles triangle inscribed in the ellipse \[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\] with its vertex at one end of the major axis.
(a) \[\dfrac{3\sqrt{3}}{4}ab\]
(b) \[\dfrac{3\sqrt{3}}{2}ab\]
(c) \[\dfrac{3}{4}ab\]
(d) \[\dfrac{3}{2}ab\]

Answer 1

Hint: In order to do these types of questions, it is very important to draw the diagram as mentioned in the figure. Here, we have drawn the ellipse with an inscribed circle as mentioned in the question. And now find the expression which maximizes and minimizes in terms of variables. So, the given equation of ellipse is \[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\] and we assume \[a >b\]. Now, we can find the area of the inscribed circle, and then we need to differentiate the area with respect to θ. After differentiating, we need to apply the concept of maxima, i.e., \[\dfrac{dA}{d\theta }=0\], and solve the equation to find the value of θ. Finally, we need to replace the value of θ in the Area of the triangle equation. This will give the maximum area.

Complete step-by-step solution:
We have to find the maximum area of an isosceles triangle inscribed in the ellipse given by the equation \[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\]. Let ABC be the triangle whose vertices are \[A\left( a,0 \right)\], \[B\left( a\cos \theta ,b\sin \theta \right)\], \[C\left( a\cos \theta ,-b\sin \theta \right)\]. Now, finding the area of \[\Delta ABC\] , we get,

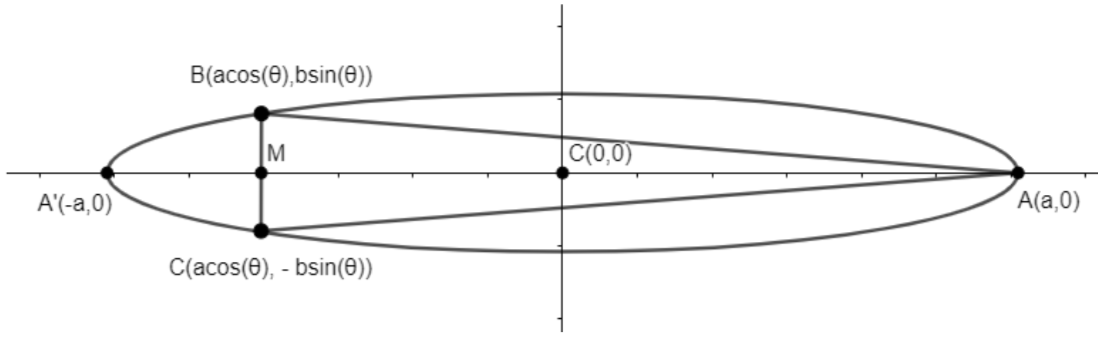
Now, Area of \[\Delta ABC,A\]\[=\dfrac{1}{2}\times \left( Base \right)\times \left( Height \right)\]
  \[=\dfrac{1}{2}\times \left( BC \right)\times \left( AB \right)\]
\[\therefore A=\dfrac{1}{2}\times \left( 2b\sin \theta \right)\times \left( a+a\cos \theta \right)\]
\[\Rightarrow A=\dfrac{1}{2}\times \left( 2ab \right)\times \sin \theta \left( 1+\cos \theta \right)\]
\[\Rightarrow A=ab\times \sin \theta \left( 1+\cos \theta \right)................(i)\]
Then, in order to get the maximum area, we have to differentiate equation (i) with respect to θ and equating it with zero, i.e., implementing the concept of maxima and minima.
We get,
\[\dfrac{dA}{d\theta }=ab\left[ \cos \theta \left( 1+\cos \theta \right)+\sin \theta \left( -\sin \theta \right) \right]=0\]
\[\Rightarrow \cos \theta +{{\cos }^{2}}\theta -{{\sin }^{2}}\theta =0\]
\[\Rightarrow \cos \theta +\cos 2\theta =0\text{ }\left[ \because {{\cos }^{2}}\theta -{{\sin }^{2}}\theta =\cos 2\theta \right]\]
Now, applying the formula \[\cos C+\cos D=2\cos \left( \dfrac{C+D}{2} \right).\cos \left( \dfrac{C-D}{2} \right)\], we get,
\[\Rightarrow 2\cos \left( \dfrac{\theta +2\theta }{2} \right).\cos \left( \dfrac{\theta -2\theta }{2} \right)=0\]
\[\Rightarrow 2\cos \left( \dfrac{3\theta }{2} \right).\cos \left( \dfrac{-\theta }{2} \right)=0\]
Since, \[\cos \left( -\theta \right)=\cos \left( \theta \right)\], so, we get,
$\Rightarrow 2\cos \left( \dfrac{3\theta }{2} \right).\cos \left( \dfrac{\theta }{2} \right)=0$
Either \[\cos \left( \dfrac{3\theta }{2} \right)=0\]
     \[\Rightarrow \cos \left( \dfrac{3\theta }{2} \right)=\cos \left( \dfrac{\pi }{2} \right)\]
     \[\Rightarrow \left( \dfrac{3\theta }{2} \right)=\left( \dfrac{\pi }{2} \right)\]
     \[\Rightarrow 3\theta =\pi \]
     \[\Rightarrow \theta =\dfrac{\pi }{3}\]
Or \[\cos \left( \dfrac{\theta }{2} \right)=0\]
\[\Rightarrow \cos \left( \dfrac{\theta }{2} \right)=\cos \left( \dfrac{\pi }{2} \right)\]
\[\Rightarrow \left( \dfrac{\theta }{2} \right)=\left( \dfrac{\pi }{2} \right)\]
\[\Rightarrow \theta =\pi \] (Not Possible)
Thus, the area of the inscribed isosceles will be maximum where \[\theta =\dfrac{\pi }{3}\]. We can also check it through second derivative test.
Substituting \[\theta =\dfrac{\pi }{3}\] in equation (i), we get,
Maximum area, \[A=ab\sin \theta \left( 1+\cos \theta \right)\]
\[\Rightarrow A=ab\times \sin \left( \dfrac{\pi }{3} \right)\times \left( 1+\cos \left( \dfrac{\pi }{3} \right) \right)\]
\[\Rightarrow A=ab\times \left( \dfrac{\sqrt{3}}{2} \right)\times \left( 1+\dfrac{1}{2} \right)\]
\[\Rightarrow A=ab\times \left( \dfrac{\sqrt{3}}{2} \right)\times \left( \dfrac{3}{2} \right)\]
\[\Rightarrow A=ab\times \left( \dfrac{3\sqrt{3}}{4} \right)\]
Hence, the correct answer is an option (a).

Note: The best approach to solve this question to draw the figure and take the coordinates in parametric form. Generally, students take coordinates in cartesian form and the entire process will get lengthy. Be careful while placing the numerical values of \[\sin \left( \dfrac{\pi }{3} \right)\] and \[\cos \left( \dfrac{\pi }{3} \right)\]. Students often makes mistake while replacing the numerical values of the corresponding trigonometric functions. Besides, students should be very careful to take while opting for the kind of form being taken while solving the equation.